
Читайте также:
|
 .
. .
. . При x→1 числитель дроби стремится к 1, а знаменатель стремится к 0. Но так как
. При x→1 числитель дроби стремится к 1, а знаменатель стремится к 0. Но так как 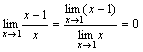 , т.е.
, т.е.  есть бесконечно малая функция при x→ 1, то
есть бесконечно малая функция при x→ 1, то 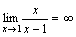 .
. Теорема 4. Пусть даны три функции f(x), u(x) и v(x), удовлетворяющие неравенствам u (x)≤f(x)≤ v(x). Если функции u(x) и v(x) имеют один и тот же предел при x→a (или x→∞), то и функция f(x) стремится к тому же пределу, т.е. если
Теорема 4. Пусть даны три функции f(x), u(x) и v(x), удовлетворяющие неравенствам u (x)≤f(x)≤ v(x). Если функции u(x) и v(x) имеют один и тот же предел при x→a (или x→∞), то и функция f(x) стремится к тому же пределу, т.е. если
 , то
, то  .
.
Смысл этой теоремы понятен из рисунка.
Доказательство теоремы 4 можно найти, например, в учебнике: Пискунов Н. С. Дифференциальное и интегральное исчисления, т. 1 – М.: Наука, 1985.
Теорема 5. Если при x→a (или x→∞) функция y=f(x) принимает неотрицательные значения y≥0 и при этом стремится к пределу b, то этот предел не может быть отрицательным: b≥0.
Доказательство. Доказательство проведем методом от противного. Предположим, что b<0, тогда |y – b|≥|b| и, следовательно, модуль разности не стремится к нулю при x→a. Но тогда y не стремится к пределу b при x→a, что противоречит условию теоремы.
Теорема 6. Если две функции f(x) и g(x) при всех значениях аргумента x удовлетворяют неравенству f(x)≥ g(x) и имеют пределы 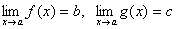 , то имеет место неравенство b≥c.
, то имеет место неравенство b≥c.
Доказательство. По условию теоремы f(x)-g(x) ≥0, следовательно, по теореме 5  , или
, или 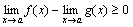 .
.
Дата добавления: 2015-09-10; просмотров: 99 | Поможем написать вашу работу | Нарушение авторских прав |