Читайте также:
|
Определение.
Дифференцируемая функция называется выпуклой вниз на интервале Х, если ее график расположен не ниже касательной к нему в любой точке интервала Х.
Определение.
Дифференцируемая функция называется выпуклой вверх на интервале Х, если ее график расположен не выше касательной к нему в любой точке интервала Х.
Выпуклую вверх функцию часто называют выпуклой, а выпуклую вниз – вогнутой.
Посмотрите на чертеж, иллюстрирующий эти определения.
Определение.
Точка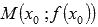 
называется точкой перегиба графика функции y=f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки 
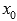, в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости.
Другими словами, точка М называется точкой перегиба графика функции, если в этой точке существует касательная и график функции меняет направление выпуклости, проходя через нее.
Если необходимо, обратитесь к разделу касательная к графику функции в точке, чтобы вспомнить условия существования невертикальной и вертикальной касательной.
На рисунке ниже представлены несколько примеров точек перегиба (отмечены красными точками). Заметим, что некоторые функции могут не иметь точек перегиба, а другие могут иметь одну, несколько или бесконечно много точек перегиба.
К началу страницы
Дата добавления: 2015-09-10; просмотров: 94 | Поможем написать вашу работу | Нарушение авторских прав |