Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Дифференциал функции

Итак, график дифференцируемой функции в окрестности каждой своей точки сколь угодно близко приближается к графику касательной в силу равенства: 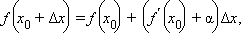где α – бесконечно малая в окрестности функция. Для приближенного вычисления значения функции f в точке x ₀ + Δ x эту бесконечно малую функцию можно отбросить:

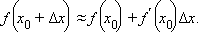
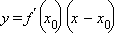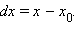Линейную функцию называют дифференциалом функции f в точке и обозначают df. Для функции x производная в каждой точке равна 1, то есть Поэтому пишут:

Приближенное значение функции вблизи точки равно сумме ее значения в этой точке и дифференциала в этой же точке. Это дает возможность записать производную следующим образом:

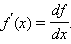
Часто эту запись используют, чтобы уточнить, по какой переменной дифференцируется функция.

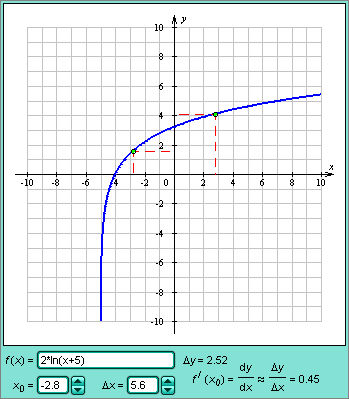
Модель 3.3. Дифференциал функции

Геометрически дифференциал функции df – это приращение ординаты касательной к графику функции в данной точке при изменении абсциссы точки на dx.