Читайте также:
|
Рассмотрим автономную систему 
и
функцию 
.
Назовем эту функцию знакоположительной, если 
,
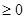знакоотрицательной, если 
Назовем функцию положительно определенной, если
она знакоположительна,
Назовем функцию отрицательно определенной, если
она знакоотрицательна,
Назовем функцию знакоопределенной, если она является отрицательно определенной или положительно определенной.
Введем производную функции в силу системы 
: 
. Заметим, что 
. Поэтому, если 
, то угол между градиентом V и вектором правых частей системы тупой. Следовательно, убывание функции V соответствует движению по фазовым траекториям внутрь линии уровня =С.
На этом основан метод функций Ляпунова. Этот метод сводится к трем теоремам Ляпунова.
Теорема Ляпунова об устойчивости. Пусть существует функция (функция Ляпунова), положительно определенная и имеющая знакоотрицательную 
в некоторой окрестности точки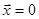 
.
Тогда тривиальное решение автономной системы 
устойчиво по Ляпунову.
Теорема Ляпунова об асимптотической устойчивости. Пусть существует функция , положительно определенная и имеющая отрицательно определенную в некоторой окрестности точки .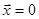
Тогда тривиальное решение автономной системы асимптотически устойчиво по Ляпунову.
Теорема Ляпунова о неустойчивости. Пусть 
. Пусть знакоопределена в некоторой окрестности точки 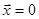. Если в любой окрестности точки 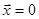найдутся такие точки, в которых знаки и совпадают, то тривиальное решение автономной системы неустойчиво.
Пример. 
Выберем 
положительно определена, отрицательно определена. Поэтому тривиальное решение асимптотически устойчиво.
Пример.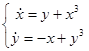 
Выберем
и положительно определены, поэтому тривиальное решение неустойчиво.
Дата добавления: 2015-09-10; просмотров: 102 | Поможем написать вашу работу | Нарушение авторских прав |