Читайте также:
|
Уравнения
Каноническое уравнение параболы в прямоугольной системе координат:
(или 
, если поменять местами оси).
| [показать]Вывод |
Квадратное уравнение 
при 
также представляет собой параболу и графически изображается той же параболой, что и 
, но в отличие от последней имеет вершину не в начале координат, а в некоторой точке 
, координаты которой вычисляются по формулам:
где D = b 2 − 4 ac - дискриминант
Уравнение может быть представлено в виде 
, а в случае переноса начала координат в точку каноническим уравнением. Таким образом для каждого квадратного уравнения можно найти систему координат такую, что в этой системе оно представляется каноническим.
править]Расчёт коэффициентов квадратного уравнения
Если для уравнения известны координаты 3-х различных точек его графика 
, 
, 
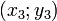, то его коэффициенты могут быть найдены так:
Дата добавления: 2015-09-10; просмотров: 121 | Поможем написать вашу работу | Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Решение неоднородных систем линейных алгебраических уравнений | | | Править]Свойства |