Читайте также:
|
Найти все функции, 
на которых функционал экстремален.
Зафиксируем все функции, кроме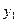 
и найдем соответствующую экстремаль.
Затем фиксируем все функции, кроме 
и т.д. Получаем систему уравнений:
Запишем граничные условия:
- числа заданны.
Пример:
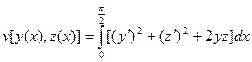
- граничные условия.
Составим систему:
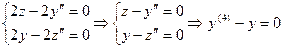Решая характеристическое уравнение, получим:
Составим ОРОУ:
Используя граничные условия, составляем систему коэффициентов:
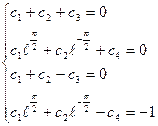находим из этой системы коэффициенты: 
Получаем:
посчитаем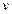 
на этих кривых и определим max это или min.
подставим 
и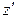 
в функционал и вычислим его.
Определим max это или min:
Возьмем две функции, удовлетворяющие граничным условиям:
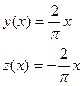
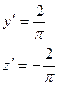подставим в функционал.
мы нашли функцию max.
Дата добавления: 2015-09-10; просмотров: 85 | Поможем написать вашу работу | Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Вариационное исчисление. | | | Функционалы, зависящие от нескольких функций и содержащие производные выше 1-го порядка. |