Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Процент, выплачиваемый p раз.

Предположим, что интенсивность процента за единицу времени постоянна и равна . Пусть и - ставка процента и дисконта соответственно.

В главе 3 мы показали, что выплачивается в момент 0, - в момент 1 и выплачивается непрерывно в интервале по постоянной ставке, и все они имеют одну и ту же стоимость. Каждый из этих платежей может рассматриваться как процент за период , выплачиваемый на заём 1, сделанный в момент 0.

Предположим, однако, что занимающий, одолживший 1 в момент 0 для выплаты в момент 1, желает платить процент по своему займу в платежей в интервале. Определим - процент, выплачиваемый раз в конце подинтервалов ; - в начале подинтервалов .

Мы можем выразить в терминах . Так как каждая процентная выплата равна , то

. (1)

Если , то

.

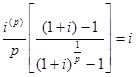Следовательно

и (2)

. (3)

Уравнения (4.1.2) и (4.1.3) наиболее важны. Любые из уравнений может быть рассмотрено как определение . Аналогично

. (4)

Для интенсивности за единицу времени следующие 5 рядов выплат на временном интервале [0;1] имеют одну и ту же стоимость.

Заметим, что и задаются непосредственно в терминах интенсивности процента :

(7)

Так как , то из (4.1.7) следует

. (8)

Легко установить, что , а . Следовательно, убывает при возрастании , а возрастает при возрастании .

Пример 4.1.4: Покажем, что если мало, то

.

Решение:

Аналогично