Читайте также:
|
Везде далее рассматриваем случай с постоянной интенсивностью процента 
. Если стоимость в момент 
, то в момент 
она составит
.
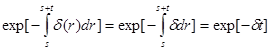Таким образом, стоимость равная 1 в любое время, становится равной
через время 
, где 
и 
определяются через 
следующим образом:
, (1)
. (2)
Таким образом, для получения 1 в момент 1 инвестор будет вкладывать 1 в момент 0. называется эффективной ставкой дисконта за 1 времени.
Из уравнения (2.4.9) следует, что аккумулируемая сумма в момент на 1, инвестированную в момент 
не зависит от и даётся
, (3)
где 
определяется уравнением
. (4)
Таким образом, инвестор будет давать взаймы сумму 1 в момент времени 0 для получения 
в момент 1.
.
Последнее равенство означает, что выплата в момент 1 имеет ту же стоимость что и выплата в момент 0. Какая сумма, выплачиваемая непрерывно на интервале 
, имеет ту же стоимость как любые из этих выплат.
Пусть искомая сумма равна 
. Тогда
, где 
.
Следовательно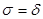 
. Этот результат справедлив и когда 
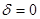. Это устанавливает важный факт, что выплата , сделанная непрерывно за период 
имеет ту же стоимость что и выплата в момент 0 или выплата в момент 1. Каждая из трёх выплат может быть рассмотрена как альтернативный способ выплаты процентов на заём 1 за период.
В некоторых ситуациях может быть естественным рассматривать интенсивность процента как основной параметр.
Если мало, то 
.
Соотношения между 
:
| величина в терминах |
|
|
|
|
|
| 
| 
| 
| |
|
| 
| 
| 
| |
|
| 
| 
| 
| |
|
| 
| 
| 
|
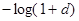
Таблица 3.1.1.
Когда мало величины и можно аппроксимировать
,
,
аналогично
.
Используя соотношения из таблицы 3.1.1, читатель должен проверить, что если мало, то
и 
.
Анализ ошибок аппроксимации на примерах.
Пример 3.1.1: Показать, что если 
, то
.
Решение: Пусть 
. Так как по теореме Тейлора
,
где 
, 
, (5)
где 
. Тогда из уравнения (3.1.5)
.
Если 
и , то
,
что и требовалось доказать.
Дата добавления: 2015-09-11; просмотров: 71 | Поможем написать вашу работу | Нарушение авторских прав |