Читайте также:
|
Цей закон, як і вся класична теорія теплоємності, протирічить наслідку з III закону термодинаміки, згідно з яким при зниженні температури до нуля будь-яка теплоємність має прямувати до нуля.
Першим це протиріччя зняв Ейнштейн, розглянувши кристал як ансамбль незалежних квантових гармонічних осциляторів з однаковою частотою 
(яку зараз називають ейнштейнівською). Це наближення досить грубе, бо, як ми бачили в попередніх параграфах, коливання атомів колективні, а їх частоти лежать у широкому інтервалі 
В моделі Ейнштейна цим нехтують, зате враховують дискретний енергетичний спектр осцилятора. Тому внутрішня енергія одного моля атомів рівна
де
(див. Част. І.
Тоді молярна теплоємність
.
Легко бачити, що при високих температурах м 
модель Ейнштейна переходить в закон Дюлонга-Пті, а при низьких дуже швидко прямує до нуля, відповідно до вимог III закону термодинаміки (рис.4.4.1). Але швидкість прямування теплоємності до нуля в моделі Ейнштейна занадто велика у порівнянні з експериментом. А саме, теплоємність діелектриків при низьких температурах пропорційна кубу температури (закон 
Дебая), теплоємність металів - лінійна комбінація кубічного та лінійного по Т доданків. (При високих температурах для обох типів твердих тіл виконується закон Дюлонга-Пті). Присутність лінійного члена в теплоємності металів, очевидно, пов'язана з квантовим фермі-газом вільних електронів (ІІ.3.2). Кубічний член в теплоємності вперше пояснив П.Дебай.
Основний крок вперед моделі Дебая у порівнянні з моделлю Ейнштейна - це врахування колективності коливань атомів у кристалі. Теплова енергія кристалу розглядається як сума середніх енергій всіх нормальних коливань
Частоти нормальних коливань розташовані дуже щільно (11.4.1, 11.4.2), тому останню суму зручніше замінити інтегралом
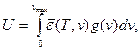
де g(v) - густина коливальних станів, тобто g(v)dv - кількість нормальних коливань з частотами з інтервалу (v,v+dv). Проблема знаходження функції g(v) є досить складною і розв'язується, в основному, чисельними методами на комп'ютері. Дебай вибрав вигляд g(v)? розглянувши кристал як неперервне пружне середовище, дискретність якого враховується лише існуванням верхньої межі частот 
(дебаєвська частота):
Вираз для §(у) записаний аналогічно до густини фотонних станів у формулі Релея- Джинса, з заміною швидкості світла на середню швидкість звуку
- швидкість повздовжніх та поперечних звукових хвиль), та з множником, який відповідає трьом можливим поляризаціям пружних хвиль замість двох поперечних поляризацій електромагнітних хвиль.
Умова нормування для g(v) з урахуванням явного виду цієї функції дає змогу знайти дебаєвську частоту
Враховуючи, що 
, де a - міжатомна відстань, маємо
,
тобто дебаєвський період 
приблизно рівний часу, за який пружна хвиля просувається на одну міжатомну відстань. У загальному випадку інтегральна формула для внутрішньої енергії не має аналітичного вигляду, але тут нас цікавлять лише два граничні випадки - високих 
і низьких 
температур. Характерну температуру 
називають дебаєвською. При високій температурі 
для всіх частот аж до дебаєвської, так що
тобто, як і можна було передбачити, отримуємо закон Дюлонга-Пті. Для випадку низьких температур
Використавши заміну 
, маємо
В останньому виразі при низьких температурах верхню межу інтегрування можна вважати нескінченною, тому інтеграл стає константою, а внутрішня енергія простою функцією температури
звідки 
Таким чином, модель Дебая правильно описує температурну залежність теплоємності твердих тіл. Сама ж температура Дебая 
виявляється границею (звичайно, досить розмитою) між квантовою 
і класичною 
поведінкою атомів у кристалі.
Ті ж самі формули Дебая можна описати дещо іншими словами. А саме, величину можна трактувати не як середню енергію осцилятора (нормальної моди) з частотою, а як енергію газу квазічастинок. енергія квазічастинки (фонона - кванту пружної енергії), яка рухається у пружному середовищі зі швидкістю звуку. Кількість фотонів з енергією яка визначається за розподілом Бозе-Ейнштейна. Фонони - це бозе-частинки, які можутьнароджуватися і зникати, а тому мають нульовий хімічний потенціал. Дійсно, але з іншого боку кількість фононів мусить відповідати рівновазі, так що Тоді внутрішню енергію кристала можна трактувати як енергію фононного газу.
Фонон є одним із прикладів елементарних збуджень конденсованого середовища. Таке уявлення може приводити задачу до добре відомих моделей - гази квазічастинок (фононів, екситонів, магнонів...) на фоні ідеального кристалу.
Дата добавления: 2015-09-11; просмотров: 80 | Поможем написать вашу работу | Нарушение авторских прав |