Читайте также:
|
Розглянемо найпростішу модель, що складається з N атомів масою т, зв'язаних пружинками (для реального кристалу атоми відповідають атомним площинам, а пружинки -квазіпружним зв'язкам між площинами при малих зміщеннях). Атоми розмістимо у вигляді ланцюжка, на який накладемо граничні періодичні умови Борна-Кармана - останній атом замкнутий на перший (рис.4.2.1), 
- коефіцієнт жорсткості пружинок, а - відстань між рівноважними вузлами ланцюжка.
Запишемо динамічні рівняння для атомів ланцюжка. Координати кожного з атомів визначаються формулою
де 
- положення п -го атома в незбуреному ланцюжку, - зміщення (як правило,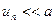 
).
Тоді для кожного атома рівняння руху матиме вигляд
де 
- потенціальна енергія системи, 
- сила, яка діє на п -й атом.
Величина V в даній моделі є сумою потенціальних енергій пружинок, в якій лише два доданки явно залежать від зміщення п -го атома. Тому
Таким чином, коливання одноатомного ланцюжка описується N диференціальними рівняннями типу
(*)
Розглядаючи 
як кінцеву різницю другого порядку, праву частину рівняння можна наближено подати у вигляді другої похідної по координаті
(**)
Отримали хвильове рівняння, яке описує поширення плоскої хвилі в неперервному середовищі. Звичайно, цим наближеним рівнянням можна користуватися лише для хвиль, довжина яких набагато більша за міжатомну відстань.
Позначивши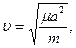 
отримаємо рівняння 
- яке має розв’язки 
, тобто рівняння плоскоїхвилі. Цей результат для наближеногорівняння (**) підказує шукати розв'язки системи динамічних рівнянь (*) у вигляді
(***)
При підстановці цього виразу для 
в (*) маємо
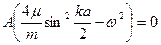
випадок А=0 (абсолютний спокій) виключаємо.
Можна зробити висновок, що розв'язок (***) задовольняє
рівнянню (*) за умови
Розглянувши геометричну інтерпретацію (рис.4.2.2) одержаного закону дисперсії, бачимо, що інтервал 
є не що інше, як перша зона Бріллюена (комірка Вігнера-Зейтца оберненої решітки
Строго кажучи, величину k не можна вибирати довільно, Оскільки на систему систему накладені граничні умови Борна-Кармана,
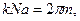
Очевидно що в першій зоні Бріллюена шириною 
реалізується N дозволених значень k
Величина k визначає проекцію хвильового вектора пружної хвилі на вісь х. Якщо хвилямає довжину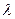 
, то
Отже,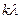 
кратне 
З іншого боку, якщо додати до хвильового вектора k період
оберненої решітки (або довільний вектор оберненої решітки й 
то закон коливання будь-якого атома не змінюеться
Таким чином додавання до вектора k з першої зони Бріллюена довільного вектора оберненої решітки не змінює стану системи - У саму хвилю. Можна зробити висновок, що всі фізично різні коливальні стани решітки вичерпуються першою зоною Бріллюена.
З закону дисперсії пружних хвиль в ланцюжку можна а фазову та групову швидкість.
Фазова швидкість (швидкість руху фронту постійної фази)
Дата добавления: 2015-09-11; просмотров: 87 | Поможем написать вашу работу | Нарушение авторских прав |