
Читайте также:
|
Теорема Крамера. Пусть  - определитель матрицы
- определитель матрицы 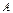 системы, а
системы, а  - определитель матрицы, получаемой из матрицы
- определитель матрицы, получаемой из матрицы 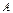 заменой
заменой  -го столбца столбцом свободных членов. Тогда, если
-го столбца столбцом свободных членов. Тогда, если  , то система имеет единственное решение, определяемое по формулам:
, то система имеет единственное решение, определяемое по формулам:
 , (
, ( ).
).
В соответствии с обратной матрицей  , где
, где  - матрица, присоединенная к матрице
- матрица, присоединенная к матрице 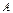 . Т.к. элементы матрицы
. Т.к. элементы матрицы  есть алгебраические дополнения элементов матрицы
есть алгебраические дополнения элементов матрицы  , транспонированной к
, транспонированной к 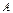 , то запишем равенство
, то запишем равенство  в развернутой форме:
в развернутой форме:
 .
.
Учитывая, что  , получим после умножения матриц:
, получим после умножения матриц:
 , откуда следует, что для любого
, откуда следует, что для любого 
 .
.
На основании свойства 9 определителей  , где
, где  - определитель матрицы, полученной из матрицы
- определитель матрицы, полученной из матрицы 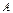 заменой
заменой  -го столбца
-го столбца  столбцом свободных членов. Следовательно
столбцом свободных членов. Следовательно  .
.
Решение системы  линейных уравнений с
линейных уравнений с  неизвестными
неизвестными
Рассмотрим систему  линейных уравнений с
линейных уравнений с  неизвестными.
неизвестными.
Теорема Кронекера-Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы:  .
.
Для совместных систем линейных уравнений верны следующие теоремы:
Теорема 1. Если ранг матрицы совместной системы равен числу переменных, т.е.  , то система имеет единственное решение.
, то система имеет единственное решение.
Теорема 2. Если ранг матрицы совместной системы меньше числа переменных, т.е.  , то система является неопределенной и имеет бесконечное множество решений.
, то система является неопределенной и имеет бесконечное множество решений.
Определение. Базисным минором матрицы называется любой ненулевой минор, порядок которого равен рангу матрицы.
Определение. Те  неизвестных, коэффициенты при которых входят в запись базисного минора, называются базисными (или основными), остальные
неизвестных, коэффициенты при которых входят в запись базисного минора, называются базисными (или основными), остальные  неизвестных называются свободными (или неосновными).
неизвестных называются свободными (или неосновными).
Решить систему уравнений в случае  - это значит выразить базисные переменные через свободные. При этом имеем общее решение системы уравнений. Если все
- это значит выразить базисные переменные через свободные. При этом имеем общее решение системы уравнений. Если все  свободные переменные равны нулю, то решение системы называется базисным.
свободные переменные равны нулю, то решение системы называется базисным.
Пример. Решить систему методом Гаусса: 
Р е ш е н и е. Выпишем и преобразуем расширенную матрицу системы. Сначала прибавим к элементам третьей строки элементы первой строки, умноженные на –1. А затем элементы второй строки умножим на –1 и прибавим к элементам третьей строки:




 .
.
Расширенная матрица приведена к ступенчатому виду.
 . Так как ранг матрицы равен 2, а количество неизвестных равно 4, то система имеет бесконечное множество решений. В качестве базисных неизвестных возьмем
. Так как ранг матрицы равен 2, а количество неизвестных равно 4, то система имеет бесконечное множество решений. В качестве базисных неизвестных возьмем  и
и  (т.к. определитель, составленный из их коэффициентов не равен нулю
(т.к. определитель, составленный из их коэффициентов не равен нулю  ), тогда
), тогда 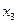 и
и 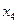 - свободные неизвестные.
- свободные неизвестные.
Выразим базисные переменные через свободные.
Из второй строки полученной матрицы выразим переменную  :
:
 ,
,  .
.
Из первой строки выразим  :
:  ,
,
 .
.
Общее решение системы уравнений:  ,
,  .
.
Дата добавления: 2015-09-11; просмотров: 86 | Поможем написать вашу работу | Нарушение авторских прав |