Читайте также:
|
В работах [37, 39, 47], положив участок пустым, т. е. m = 0, из (2.13) получают выражение (2.1). Далее из единицы вычитают (2.1) и получают вероятность отказа (2.2). Выражения (2.1) и (2.2) образуют полную группу несовместных событий, которая при таких операциях и не может не равняться единице, так как
.
Но распределение Пуассона построено применительно к вероятности реализации дискретного числа ровно m событий (точек) на участке от 0 до t. Длина участка t в распределении Пуассона не является независимой переменной, а входит как сомножитель в параметр распределения a = λ t.
Именно на то, что в теории надежности вероятность безотказной работы получена в виде (2.1) из выражения (2.13) при m = 0 и стоит обратить особое внимание.
Во-первых, распределение Пуассона получено в теории вероятностей как распределение событий попадания точек (отказов) на интервал, а безотказная работа - отсутствие событий. Такое преобразование распределения следует считать неправомерным.
Во-вторых, распределение Пуассона определяет «вероятность попадания того либо иного числа точек на отрезок», а ноль не является числом натурального ряда. Натуральный ряд чисел описывается сочетанием 10 цифр от 0 до 9. Цифр 10, но ряд начинается с числа 1, т.к. 0 обозначает отсутствие количества.
В-третьих, при m = 0 из выражения (2.13) исчезает переменная m и одновременно выполняется ее прямая замена на переменную t. Замена в (2.13) переменной m на t возможна, но с использованием преобразования Лапласа. В этом случае будет получено не экспоненциальное, а гамма- распределение [48].
Рассмотрим вероятность попадания одной точки (реализация одного отказа) на участок 
. При 
вероятность отказа будет иметь вид
. (2.14)
Вероятности 
из (2.1) и 
из (2.14) образуют полную группу несовместных событий, но
+ 
= 
. (2.15)
Поскольку и все же представляют собой полную группу несовместных событий, то их сумма должна быть равна 1, но условие не выполняется.
График суммы (2.15) приведен на рис. 2.8
Рисунок 2.8 – Зависимость суммы + от времени
В действительности в теории вероятностей [39,49] выражение (2.2) рассматривается как вероятность не одного, а одного и более отказов. В этом случае условие (2.15) выполняется, но в другой записи
, (2.16)
где m – число точек попадания (отказов) на отрезок [0, t ].
На рисунке 2.9 приведены кривые, среди которых значение вероятностей отказов 
, рассчитано по выражению (2.2), полученному из распределения Пуассона (2.13) для случая m = 0. Остальные кривые получены непосредственно из выражения (2.13) при различных числах отказов (m = 1, 2, 3, 4). Кривая 
получена для 10 отказов в результате суммирования 
.
Рисунок 2.9 – Вероятности отказа агрегата определенные при различных m
В теории вероятностей в распределении Пуассона (2.13) вероятность попадания определенного числа точек m на участок времени протяженностью t обозначается как 
. В теории надежности, вероятность попадания точки на участок отождествляется с вероятностью отказа и обозначается как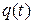 
. Поэтому вместо обозначения из (2.13), используется 
, где m, как и в распределении Пуассона, обозначает число точек попадающих на рассматриваемый участок.
Анализ рис. 2.9 показывает, что в соответствии с распределением Пуассона, вероятности отказов 
и , совпадают при t изменяющемся от 0 до 5. Для обеспечения совпадения в большем диапазоне t необходимо увеличить число членов суммы.
В связи с изложенным, встает вопрос, каким образом вероятность отказа 
, определенная по (2.2) при m =0, фактически совпадает с вероятностью большого числа отказов? Модели (2.1) и (2.2) используются в теории надежности для оценки свойства надежности отдельного агрегата, который не может иметь более одного отказа. В связи с этим, можно утверждать, что выражения (2.1) и (2.2) неадекватно оценивают надежность отдельного агрегата. Подобная некорректность возникла вследствие того, что для оценки надежности отдельного агрегата использовано распределение Пуассона, при построении которого не ставилась и не решалась задача оценки вероятности одного, либо первого отказа в функции времени.
В работе [48] задача Пуассона о попадании m точек на отрезок оси x решена с использованием марковских процессов, марковских цепей и преобразований Лапласа. В итоге получено выражение вида (2.13) относительно вероятности ровно k отказов группы из n агрегатов на отрезке времени [0, t ]. Попутно следует подчеркнуть, что полученное из выражения Пуассона значение вероятности одного отказа (2.14) не единственное, поскольку находится в совокупности вероятностей 2, 3, …, k отказов на отрезке времени [0, t ]. По этой причине вероятность одного отказа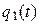 
достигает максимального значения 0,37 при λ× t =100. Вероятности 2,3, …, k отказов в сумме приближаются к 0,63 при k ®∞/
При построении распределения Пуассона ставилась и решалась задача об определении вероятностей попадания на отрезок определенной протяженности ровно m точек. В теории надежности ее постановка другая. Необходимо определить вероятность попадания на отрезок первой и единственной точки. Таким образом, использование распределения Пуассона для определения вероятности первого и единственного отказа агрегата в экспоненциальной форме вызвано ошибочной подменой задач на этапе их постановки. Покажем это.
С увеличением протяженности отрезка вероятность реализации на нем одной точки уменьшается, а большого числа точек – возрастает. При этом, ответ на вопрос с какой вероятностью и на каком расстоянии от начала рассматриваемого отрезка появится первая точка (отказ) распределение Пуассона не дает. Положим в выражении (2.13) 
, а t =100 часам. Рассчитаем вероятности попадания на отрезок t ровно m точек. При этом ужесточим условие стационарности, положив, что точки распределены по отрезку не с одинаковой средней плотностью, а равномерно. На рис. 2.10 показано такое расположение точек.
В соответствии с предположением о вероятности попадания на отрезок t =100 часов хотя бы одной точки (m =1) вероятность такого события
.
Рисунок 2.10 – Схема равномерного распределения точек на отрезке и
вероятности их реализаций рассчитанные по выражению (2.13)
В то же время вероятность попадания первой точки на отрезок в двое меньший, т.е. t =50 часов (рис. 2.10) будет
1- p (0)- p (1)=0,801,
а вероятность попадания на отрезок протяженностью 25 часов
1- p (0)- p (1)- p (2)- p (3)=0,2983.
При этом на отрезке в 100 часов вероятность попадания первой точки реализуется в первом случае дважды, а во втором четырехкратно.
Естественно, что при распределении с одинаковой средней плотностью распределение точек на отрезке в 100 часов будет несколько отличным от рис. 2.10, но в силу условия стационарности и ординарности отличие будет не кардинальным.
При экспоненциальном распределении вероятность отказа стремится к 1 при 
. С точки зрения математики, на первый взгляд, с этим можно согласиться, но практика убеждает нас в том, что любой агрегат с вероятностью 1 откажет на ограниченном отрезке времени. Приняв в выражении (2.2) и (2.13) 
мы согласились с тем, что поток отказов стационарный Пуассоновский. Из выражения (2.13) прямо следует, что вероятность одного отказа при , т.е. на бесконечно большом отрезке, стремится к 0. А максимальной, при , становится вероятность бесконечно большого числа отказов. Следовательно, вероятность не только одного, но и первого отказа достигается на ограниченном отрезке. Это хорошо согласуется с отказами агрегатов, наблюдаемыми на практике в эксплуатации функциональных систем самолетов.
Распределение Пуассона в руководствах по статистике часто фигурирует под названием «закона редких явлений». На практике показано [97], что при большом числе опытов и малой вероятности появления события в каждом отдельном опыте число появления событий приближенно подчиняется закону Пуассона, но не экспоненциальному.
***
В связи с изложенным, получение экспоненциального распределения из распределения Пуассона следует признать некорректным.
Дата добавления: 2015-09-10; просмотров: 106 | Поможем написать вашу работу | Нарушение авторских прав |