
Читайте также:
|
Пример 1
По 30 территориям России имеются данные, представленные в табл. 2.1.
Таблица 2.1
| Признак | Среднее значение | Среднее квадратическое отклонение | Линейный коэффициент парной корреляции |
| Среднедневной душевой доход, руб., у | 86,8 | 11,44 | - |
| Среднедневная заработная плата одного работающего, руб., х1 | 54,9 | 5,86 | ryx1 = 0,8405 |
| Средний возраст безработного, лет, x2 | 33,5 | 0,58 | ryx2 = -0,2101 rx1x2 = -0,1160 |
Требуется:
1. Построить уравнение множественной регрессии в стандартизованной и естественной форме; рассчитать частные коэффициенты эластичности, сравнить их с β1 и β2, пояснить различия между ними.
2. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции, сравнить их с линейными коэффициентами парной корреляции, пояснить различия между ними.
3. Рассчитать общий и частные F-критерии Фишера.
Решение
Линейное уравнение множественной регрессии у от x1 и х2 имеет вид: y = a + b1 · x1 + b2 · x2. Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизованном масштабе: ty = β · tx1 + β2 ·t x2
Расчет β - коэффициентов выполним по формулам

Получим уравнение
ty = 0,8273 t x1 - 0,114 t x2
Для построения уравнения в естественной форме рассчитаем b1 и b2, используя формулы для перехода от β i к bi,:

Значение a определим из соотношения
a = y - b1 · x1 - b2 · x2 = 86,8 - 1,6151 · 54,9 + 2,2505 · 33,5 = -73,52276,
y x1x2 = -73,52 + 1,62 · x1 - 2,25 · x2
Для характеристики относительной силы влияния х1 и х2 на у рассчитаем средние коэффициенты эластичности:

С увеличением средней заработной платы x1 на 1% от ее среднего уровня средний душевой доход у возрастает на 1,02% от своего среднего уровня; при повышении среднего возраста безработного х2 на 1% среднедушевой доходу снижается на 0,87% от своего среднего уровня. Очевидно, что сила влияния средней заработной платы х1 на средний душевой доход у оказалась большей, чем сила влияния среднего возраста безработного х2 К аналогичным выводам о силе связи приходим при сравнении модулей значений β1 и β2:
|β1 | = |0,8273| > |β2 | = |- 0,1141 |
Различия в силе влияния фактора на результат, полученные при сравнении Э yx j и β j, объясняются тем, что коэффициент эластичности исходит из соотношения средних:. Э yx j = b j
| x j |
| y |
- β коэффициент - из соотношения средних квадратических отклонений: β i = b i
| σ xi |
| σy |
2. Линейные коэффициенты частной корреляции здесь рассчитываются по рекуррентной формуле:

Если сравнить значения коэффициентов парной и частной корреляции, то приходим к выводу, что из-за слабой межфакторной связи (rx1x2 = -0,116) коэффициенты парной и частной корреляции отличаются незначительно: выводы о тесноте и направлении связи на основе коэффициентов парной и частной корреляции совпадают:
ryx1=0,8405; ryx2 = -0,2101; r x1x2 = 0,1160;
ryx1 · x2=0,8404; ryx2 · x1 = -0,2092; ryx1x2 · y = 0,1144.
Расчет линейного коэффициента множественной корреляции выполним с использованием коэффициентов ryxj. и β j:

Зависимость у от x1 и x2 характеризуется как тесная, в которой 72% вариации среднего душевого дохода определяются вариацией учтенных в модели факторов: средней заработной платы и среднего возраста безработного. Прочие факторы, не включенные в модель, составляют соответственно 28% от общей вариации у.
3. Общий F-критерий проверяет гипотезу Н о о статистической значимости уравнения регрессии и показателя тесноты связи (R2 = 0):

Fтабл = 3,4; α = 0,05
Сравнивая Fтабл и Fфакт, приходим к выводу о необходимости отклонить гипотезу H0, так. как Fтабл = 3,4 < F факт = 34,6. С вероятностью 1 - а = 0,95 делаем заключение о статистической значимости уравнения в целом и показателя тесноты связи Ryx1x2 которые сформировались под неслучайным воздействием факторов х1 и х2.
Частные F-критерии - Fx1 и F X 2 оценивают статистическую значимость присутствия факторов x1 и х2 в уравнении множественной регрессии, оценивают целесообразность включения в уравнение одного фактора после другого фактора, т.е. Fx1 оценивает целесообразность включения в уравнение фактора х1 после того, как в него был включен фактор x2. Соответственно Fx 2 указывает на целесообразность включения в модель фактора x2 после фактора х1:

Fтабл = 4,21; α = 0,05.
Сравнивая Fтабл и Fфакт, приходим к выводу о целесообразности включения в модель фактора x1 после фактора х2, так как F x1 факт= 64,9>FTaбл. Гипотезу H0 о несущественности прироста R2 Y за счет включения дополнительного фактора х1 отклоняем и приходим к выводу о статистически подтвержденной целесообразности включения фактора х1 после фактора x2.
Целесообразность включения в модель фактора х2 после фактора x1 проверяет F x2:

Низкое значение Fx2 факт (немногим больше 1) свидетельствует о статистической незначимости прироста r2yx1 за счет включения в модель фактора х2 после факторах. Следовательно, подтверждается нулевая гипотеза H0 о нецелесообразности включения в модель фактора x2 (средний возраст безработного). Это означает, что парная регрессионная модель зависимости среднего дохода от средней заработной платы является достаточно статистически значимой, надежной и что нет необходимости улучшать ее, включая дополнительный фактор х2 (средний возраст безработного).
Пример 2
По 20 территориям России изучаются следующие данные (табл. 2.2): зависимость среднегодового душевого дохода у (тыс. руб.) от доли занятых тяжелым физическим трудом в общей численности занятых x1 (%) и от доли экономически активного населения в численности всего населения х2 (%).
Таблица 2.2
| Признак | Среднее значение | Среднее квадратическое отклонение | Характеристика тесноты связи | Уравнение связи |
| y | 112,76 | 31,58 | Ryx1x2=0,773 | ŷ x1x2 = -130,49 + 6,14·x1 + 4,13 ·x2 |
| x1 | 5,40 | 3,34 | ryx1 = 0,746 | ŷ x1 = 74,4+7,1·x1 |
| x2 | 50,88 | 1,74 | r yx2=0,507 rx1x2 = 0,432 | ŷ x2 = -355,3 + 9,2 · x2 |
Требуется:
1. Составить таблицу дисперсионного анализа для проверки при уровне значимости α= 0,05 статистической значимости уравнения множественной регрессии и его показателя тесноты связи.
2. С помощью частных F-критериев Фишера оценить, насколько целесообразно включение в уравнение множественной регрессии фактора X1 после фактора Х2 и насколько целесообразно включение X2 после X1
3. Оценить с помощью t-критерия Стьюдента статистическую значимость коэффициентов при переменных X1 и X2 множественного уравнения регрессии.
Решение
1. Задача дисперсионного анализа состоит в проверке нулевой гипотезы HQ о статистической незначимости уравнения регрессии в целом и показателя тесноты связи.
Анализ выполняется при сравнении фактического и табличного (критического) значений F-критерия Фишера Fтабл и Fфакт. Fфакт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы

где n- число единиц совокупности; т - число факторов в уравнении линейной регрессии; ŷ -фактическое значение результативного признака; y х1х2 - расчетное значение результативного признака.
Результаты дисперсионного анализа представлены в табл. 2.3.
Таблица 2.3
| Вариация результата, у | Число степеней свободы | Сумма квадратов отклонений, S | Дисперсия на одну степень свободы, S2 | Fфакт | Fтабл α = 0,05 k1 = 2,k2 = 17 |
| Общая | dƒ = n - 1 = 19 | 19945,9 | - | - | - |
| Факторная | k1 = m = 2 | 11918,3 | 5959,15 | 12,62 | 3,59 |
| Остаточная | k2 = n - m - 1 = 17 | 8027,6 | 472,21 | - | - |

Сравнивая Fтабл и Fфакт, приходим к выводу о необходимости отклонить гипотезу H0 и сделать вывод о статистической значимости уравнения регрессии в целом и значения R2 yx1x2, так как они статистически надежны и сформировались под систематическим действием неслучайных причин. Вероятность того, что допускаются ошибки при отклонении нулевой гипотезы, не превышает 5%, и это является достаточно малой величиной.
2. Частный F-критерий Фишера оценивает статистическую целесообразность включения фактора х1 в модель после того, как в нее включен фактор x2. Частный F-критерий Фишера строится как отношение прироста факторной дисперсии за счет дополнительно включенного фактора (на одну степень свободы) к остаточной дисперсии (на одну степень свободы), подсчитанной по модели с включенными факторами х1 и х2
Fчастнx1 =
| Sфактyx1x2 - Sфактyx2 |
| Sост yx1x2 |
·
| n - m - 1 |
Результаты дисперсионного анализа представлены в табл. 2.4.
Таблица 2.4
| Вариация результата, у | Число степеней свободы | Сумма квадратов отклонений S | Дисперсия на одну степень свободы, S2 | Fфакт | Fтабл α = 0,05, k1=2 k2=17 |
| Общая | dƒ = n - 1 = 19 | 19945,9 | - | - | - |
| Факторная В том числе: | k1= т = 2 | 11918,3 | 5959,15 | 12,62 | 3,59 |
| за счет х2 | 5127,1 | 5127,1 | 10,86 | 4,45 | |
| за счет дополнительно включенного х1 | 6791,2 | 6791,2 | 14,38 | 4,45 | |
| Остаточная | k2 = n - m -1 = 17 | 8027,6 | 472,21 | - | - |
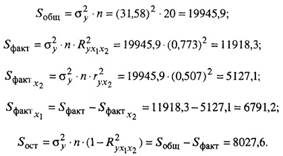
Включение фактора х1 после фактора х2 оказалось статистически значимым и оправданным: прирост факторной дисперсии (в расчете на одну степень свободы) оказался существенным, т.е. следствием дополнительного включения в модель систематически действующего фактора x1 так как F частн x1 = 14,38 > Fтабл = 4,45.
Аналогично проверим целесообразность включения в модель дополнительного фактора х2 после включенного ранее фактора х1. Расчет выполним с использованием показателей тесноты связи
R2 yx1x2 и r2 yx 1 .

В силу того что F частн x 2 = 1,73 < Fтабл = 4,45, приходим к выводу, что включение х2 после х1 оказалось бесполезным: прирост факторной дисперсии в расчете на одну степень свободы был несуществен, статистически незначим, т.е. влияние х2 не является устойчивым, систематическим. Вполне возможно было ограничиться построением линейного уравнения парной регрессии у от х1.
3. Оценка с помощью t-критерия Стьюдента значимости коэффициентов b1 и b2 связана с сопоставлением их значений с величиной их случайных ошибок: mb1 и тb2. Расчет значений случайных ошибок достаточно сложен и трудоёмок. Поэтому предлагается более простой способ: расчет значения t-критерия Стьюдента для коэффициентов регрессии линейного уравнения как квадратного корня из соответствующего частного F-критерия Фишера:

Табличные (критические) значения f-критерия Стьюдента зависят от принятого уровня значимости а (обычно это 0,1; 0,05 или 0,01) и от числа степеней свободы (п - т - 1), где п - число единиц совокупности, т - число факторов в уравнении.
В нашем примере при α = 0,05; df= 20 - 3 = 17; tтабл = 2,10. Сравнивая t табл и tфакт, приходим к выводу, что так как t b1 = 3,79 > 2,11 = tтабл коэффициент регрессии b1 является статистически значимым, надежным, на него можно опираться в анализе и в прогнозе. Так как t b2 = 1,32 < 2,10 = tтаблприходим к заключению, что величина b2 является статистически незначимой, ненадежной в силу того, что она формируется преимущественно под воздействием случайных факторов. Еще раз подтверждается статистическая значимость влияния х1 (доли занятых тяжелым физическим трудом) на у (среднедушевой доход) и ненадежность, незначимость влияния х2 (доли экономически активного населения в численности всего населения).
Пример 3
Зависимость спроса на свинину х1 от цены на нее х2 и от цены на говядину хз представлена уравнением
lgxl =0,1274 -0,2143 -Igx2 +2,8254 -Igx3
Требуется:
1. Представить данное уравнение в естественной форме (не в логарифмах).
2. Оценить значимость параметров данного уравнения, если известно, что t-критерий для параметра b2 при х2 составил 0,827, а для параметра b3 при х3 - 1,015.
Решение
1. Представленное степенное уравнение множественной регрессии приводим к естественной форме путём потенцирования обеих частей уравнения:
x1 = 100,1274 · x2-0,2143 · x32,8254;
x1 = 1,3409 ·
| x20,2143 |
· x32,8254;
Значения коэффициентов регрессии b1 и b2 в степенной функции равны коэффициентам эластичности результатах! От x2 и х3.
Э x1x2 = -0,2143 %; Э x1x3 = 2,8254 %
Спрос на свинину х1 сильнее связан с ценой на говядину - он увеличивается в среднем на 2,83% при росте цен на 1%. С ценой на свинину спрос на нее связан обратной зависимостью: с ростом цен на 1% потребление снижается в среднем на 0,21%.
2. Табличное значение r-критерия для α = 0,05 обычно лежит в интервале 2 - 3 - в зависимости от степеней свободы. В данном примере tb2 = 0,827, tb3 = 1,015. Это весьма небольшие значения t-критерия,
которые свидетельствуют о случайной природе взаимосвязи, о статистической ненадежности всего уравнения, поэтому применять полученное уравнение для прогноза не рекомендуется.
Пример 4
По 20 предприятиям региона (табл. 2.5) изучается зависимость выработки продукции на одного работника у (тыс. руб.) от ввода в действие новых основных фондов х1 (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих x2 (%).
Таблица 2.5
| Номер предприятия | y | x1 | x2 | Номер предприятия | y | x1 | Х2 |
| 7,0 | 3,9 | 10,0 | 9,0 | 6,0 | 21,0 | ||
| 7,0 | 3,9 | 14,0 | 11,0 | 6,4 | 22,0 | ||
| 7,0 | 3,7 | 15,0 | 9,0 | 6,8 | 22,0 | ||
| 7,0 | 4,0 | 16,0 | 11,0 | 7,2 | 25,0 | ||
| 7,0 | 3,8 | 17,0 | 12,0 | 8,0 | 28,0 | ||
| 7,0 | 4,8 | 19,0 | 12,0 | 8,2 | 29,0 | ||
| 8,0 | 5,4 | 19,0 | 12,0 | 8,1 | 30,0 | ||
| 8,0 | 4,4 | 20,0 | 12,0 | 8,5 | 31,0 | ||
| 8,0 | 5,3 | 20,0 | 14,0 | 9,6 | 32,0 | ||
| 10,0 | 6,8 | 20,0 | 14,0 | 9,0 | 36,0 |
Требуется:
1. Оценить показатели вариации каждого признака и сделать вывод о возможностях применения МНК для их изучения.
2. Проанализировать линейные коэффициенты парной и частной корреляции.
3. Написать уравнение множественной регрессии, оценить значимость его параметров, пояснить их экономический смысл.
4. С помощью F-критерия Фишера оценить статистическую надежность уравнения регрессии и R2 yx1x2 Сравнить значения скорректированного и нескорректированного линейных коэффициентов множественной детерминации.
5. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора х1 после x2 и фактора x2 после x1
6. Рассчитать средние частные коэффициенты эластичности и дать на их основе сравнительную оценку силы влияния факторов на результат.
2.3. РЕАЛИЗАЦИЯ ТИПОВЫХ ЗАДАЧ НА КОМПЬЮТЕРЕ
1. Решение примера проведем с использованием ППП MS Excel и Statgraphics.
Решение с помощью ППП Excel
Сводную таблицу основных статистических характеристик для одного или нескольких массивов данных можно получить с помощью инструмента анализа данных Описательная статистика. Для этого выполните следующие шаги:
1) введите исходные данные или откройте существующий файл, содержащий анализируемые данные;
2) в главном меню выберите последовательно пункты Сервис /Анализ данных / Описательная статистика, после чего щелкните по кнопке ОК;

Рис. 2.1. Диалоговое окно ввода параметров инструмента Описательная статистика
3) заполните диалоговое окно ввода данных и параметров вывода
(рис. 2.1):
Входной интервал, - диапазон,, содержащий анализируемые данные, это может быть одна или несколько строк (столбцов); Группирование - по столбцам или по строкам - необходимо указать дополнительно;
Метки - флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Выходной интервал - достаточно указать левую верхнюю ячейку будущего диапазона;
Новый рабочий чист - можно задать произвольное имя нового листа.
Если необходимо получить дополнительную информацию Итоговой статистики, Уровня надежности, k-гo наибольшего и наименьшего значений, установите соответствующие флажки в диалоговом окне. Щелкните по кнопке ОК
Результаты вычисления соответствующих показателей для каждого признака представлены на рис. 2 2

Рис. 2.2. Результат применения инструмента Описательная статистика
Решение с помощью ППП Statgraphics
Для проведения многофакторного анализа в ППП Statgraphics используется пункт меню Multiple Variable Analysis. Для получения показателей описательной статистики необходимо проделать следующие операции:
1) ввести исходные данные или открыть существующий файл, содержащий анализируемые данные,
2) в главном меню выбрать Describe/Numeric Data/Multiple Variable Analysis,
3) заполнить диалоговое окно ввода данных (рис. 2 3) Ввести названия всех столбцов, значения которых вы хотите включить в анализ;щелкнуть по кнопке ОК,

Рис. 2.3. Диалоговое окно ввода данных
4) в окне табличных настроек поставить флажок напротив Summary Statistics (рис 2 4) Итоговая статистика - показатели вариации -появится в отдельном окне

Рис. 2.4.Окно табличных настроек Multiple Variable Analysis
Для данных примера 4 результат применения функции Multiple Variable Analysis представлен на рис 2.5
 :
:
Рис. 2.5. Итоговая статистика
Сравнивая значения средних квадратических отклонений и средних величин и определяя коэффициенты вариации:

приходим к выводу о повышенном уровне варьирования признаков, хотя и в допустимых пределах, не превышающих 35%. Совокупность предприятий однородна, и для ее изучения могут использоваться метод наименьших квадратов и вероятностные методы оценки статистических гипотез.
2. Значения линейных коэффициентов парной корреляции определяют тесноту попарно связанных переменных, использованных в данном уравнении множественной регрессии. Линейные коэффициенты частной корреляции оценивают тесноту связи значений двух переменных, исключая влияние всех других переменных, представленных в уравнении множественной регрессии.
Решение с помощью ППП Excel
К сожалению, в ППП MS Excel нет специального инструмента для расчета линейных коэффициентов частной корреляции. Матрицу парных коэффициентов корреляции переменных можно рассчитать, используя инструмент анализа данных Корреляция. Для этого:
1) в главном меню последовательно выберите пункты Сервис / Анализ данных / Корреляция. Щелкните по кнопке ОК;
2) заполните диалоговое окно ввода данных и параметров вывода (см. рис. 2.1);
3) результаты вычислений - матрица коэффициентов парной корреляции - представлены на рис. 2.6.

Рис. 2.6. Матрица коэффициентов парной корреляции
Решение с помощью ППП Statgraphics
При проведении многофакторного анализа - Multiple Variable Analysis - вычисляются линейные коэффициенты парной корреляции и линейные коэффициенты частной корреляции. Последовательность операций описана в п.1 этого примера. Для отображения результатов вычисления на экране необходимо установить флажки напротив Correlations и Partial Correlations в окне табличных настроек (рис. 2.7).

Рис.2.7. Окно табличных настроек Multiple Variable Analysis
В результате получим матрицы коэффициентов парной и частной корреляции (рис 2 8)

Рис. 2.8 Матрицы коэффициентов парной и частной корреляции
Значения коэффициентов парной корреляции указывают на весьма тесную связь выработки у как с коэффициентом обновления основных фондов.- х1, так и с долей рабочих высокой квалификации - х2 (ryx1 = 0,9699 и r уx2 = 0,9408). Но в то же время межфакторная связь r x1 x2 = 0,9428 весьма тесная и превышает тесноту связи х2 с у. В связи с этим для улучшения данной модели можно исключить из нее фактор х2 как малоинформативный, недостаточно статистически надежный.
Коэффициенты частной корреляции дают более точную характеристику тесноты связи двух признаков, чем коэффициенты парной корреляции, так как очищают парную зависимость от взаимодействия данной пары признаков с другими признаками, представленными в модели. Наиболее тесно связаны у и х1: ryx1 ·x2 = 0,7335, связь у и x2 гораздо слабее: ryx2 · x 1 = 0,3247, а межфакторная зависимость х1 и х2 выше, чем парная у и х2: r yx2 · x 1 = 0,3247 < rx1x2 · y = 0,3679. Все это приводит к выводу о необходимости исключить фактор х2 - доля высококвалифицированных рабочих - из правой части уравнения множественной регрессии.
Если сравнить коэффициенты парной и частной корреляции, то можно увидеть, что из-за высокой межфакторной зависимости коэффициенты парной корреляции дают завышенные оценки тесноты связи:
ryx1 = 0,9699; ryx1 · x2 = 0,7335; ryx2 = 0,9408;
ryx2 · x1 = 0,3247.
Именно по этой причине рекомендуется при наличии сильной коллинеарности (взаимосвязи) факторов исключать из исследования тот фактор, у которого теснота парной зависимости меньше, чем теснота межфакторной связи.
3. Вычисление параметров линейного уравнения множественной регрессии.
Решение с помощью ППП Excel
Эта операция проводится с помощью инструмента анализа данных Регрессия. Она аналогична расчету параметров парной линейной регрессии, описанной в 1-м разделе практикума, только в отличие от парной регрессии в диалоговом окне при заполнении параметра входной интервал X следует указать не один столбец, а все столбцы, содержащие значения факторных признаков. Результаты анализа представлены на рис. 2.9.

Рис. 2.9.Результат применения инструмента Регрессия
Решение с помощью ППП Statgraphics
Для вычисления параметров множественной регрессии можно использовать процедуру Multiple Regression. Для этого:
1) введите исходные данные или откройте существующий файл;
2) в главном меню последовательно выберите Relate / Multiple Regression;
3) заполните диалоговое окно ввода данных. В поле Depended Variable введите название столбца, содержащего значения зависимой переменной, в поле Independed Variable - названия столбцов, содержащих значения факторов. Щелкните по кнопке ОК.
Результаты вычисления функции Multiple Regression появятся в отдельном окне (рис. 2.10).
По результатам вычислений составим уравнение множественной регрессии вида
ŷ = b0 + b1 · x1 + b2 · x2
ŷ = 1,8353 + 0,9459 · x1 + 0,0856 · x2
Значения случайных ошибок параметров b0, b1 и b2 с учетом округления:
mb0 = 0,4711; mb1 = 0,2126; mb2 = 0,0605.
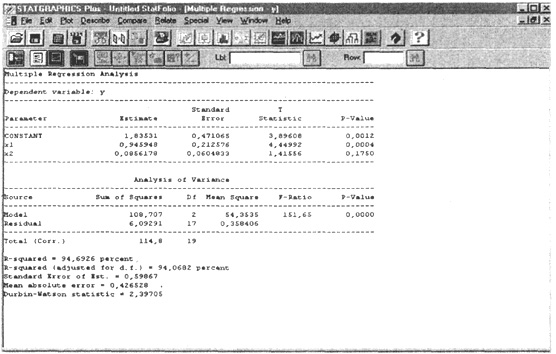
Рис. 2.10. Итоговое окно функцииMultiple Regression
Они показывают, какое значение данной характеристики сформировалось под влиянием случайных факторов. Эти значения используются для расчета t-критерия Стьюдента:
t b0 = 3,90; t b1 = 4,45; tb2 = 1,42.
Если значения r-критерия больше 2-3, можно сделать вывод о существенности данного параметра, который формируется под воздействием неслучайных причин. Здесь статистически значимыми являются и b1, а величина b2, сформировалась под воздействием случайных причин, поэтому фактор х2, силу влияния которого оценивает b2, можно исключить как несущественно влияющий, неинформативный.
На это же указывает показатель вероятности случайных значений параметров регрессии: если а меньше принятого нами уровня (обычно 0,1; 0,05 или 0,01; это соответствует 10%; 5% или 1% вероятности), делают вывод о неслучайной природе данного значения параметра, т.е. о том, что он статистически значим и надежен. В противном случае принимается гипотеза о случайной природе значения коэффициентов уравнения. Здесь αx2 = 17,5 % >5%, что позволяет рассматривать x2 как неинформативный фактор и удалить его для улучшения данного уравнения.
Величина b0 оценивает агрегированное влияние прочих (кроме учтенных в модели факторов х1 и x2) факторов на результат y
Величины b1 и b2 указывают, что с увеличением х1 и х2 на единицу их значений результат увеличивается соответственно на 0,9459 и на 0,0856 млн руб. Сравнивать эти значения не следует, так как они зависят от единиц измерения каждого признака и потому несопоставимы между собой.
4.Оценку надежности уравнения регрессии в целом и показателя тесноты связи Ryx1x2 дает F-критерий Фишера:
F факт =
| ∑(ŷx1x2 - y)2 |
| m |
:
| ∑(y - ŷx1x2)2 |
| n - m - 1 |
По данным таблиц дисперсионного анализа, представленным на рис. 2.9 и 2.10, Fфакт = 151,65. Вероятность случайно получить такое значение F-критерия составляет 0,0000, что не превышает допустимый уровень значимости 5%; об этом свидетельствует величина Р - значения из этих же таблиц. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т.е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи R2yx1x2 .
Значения скорректированного и нескорректированного линейных коэффициентов множественной детерминации приведены на рис. 2.9 и 2.10 в рамках регрессионной статистики.
Нескорректированный коэффициент множественной детерминации R2 yx1x2 = 0,9469 оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 94,7% и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, иными словами - на весьма тесную связь факторов с результатом.
Скорректированный коэффициент множественной детерминации
Ř2 yx1x2 = 0,9407 определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и потому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на весьма высокую (более 90%) детерминированность результата^ в модели факторами x1 и х2.
5. Информация для оценки с помощью частных F-критериев Фишера целесообразности включения в модель фактора х1 после фактора х2 ифактора x2 после фактора х1 может быть получена в ППП Statgraphics следующим образом:
1) введите исходные данные или откройте существующий файл;
2) в главном меню последовательно выберите пункты Relate / Multiple Regression;
3) заполните диалоговое окно ввода данных. В поле Depended Variable введите название столбца, содержащего значения зависимой переменной, в поле Independed Variable - названия столбцов, содержащих значения факторов, в том порядке, в котором будет проводиться анализ целесообразности включения факторов в модель. Чтобы оценить статистическую значимость включения в модель фактора х1 после фактора х2, сначала введите фактор х1, затем х2. Для оценки обратного порядка включения факторов в модель х2 после х1 введите х2, затем x1. Щелкните по кнопке ОК;
4) в окне табличных настроек поставьте флажок напротив поля Conditional Sums of Squares.
Результаты вычисления показаны на рис. 2.11.

Рис. 2.11. Результаты вычисления частных F-критериев Фишера
Частный F-критерий - Fчастнx2 показывает статистическую значимость включения фактора x2 в модель после того, как в нее включен фактор х1.
Fчастнx2 Вероятность случайной природы его значения (Р - значение = 0,1750) составляет 17,5% против принятого уровня значимости α = 0,05, (5%). Следовательно, включение в модель фактора х2 - доля высококвалифицированных рабочих - после того, как в уравнение включен фактор х1 - коэффициент обновления основных фондов - статистически нецелесообразно: прирост факторной дисперсии за счет дополнительного признака х2 оказывается незначимым, несущественным; фактор х2 включать в уравнение после фактора х1 не следует.
Если поменять первоначальный порядок включения факторов в модель и рассмотреть вариант включения х1 после х2, то результат расчета частного F-критерия для х1 будет иным. Fчacтн x1 = 19,80.
Вероятность его случайного формирования составила 0,04%, это значительно меньше принятого стандарта α = 0,05 (5%). Следовательно, значение частного F-критерия для дополнительно включенного фактора x1 не случайно, является статистически значимым, надежным, достоверным: прирост факторной дисперсии за счет дополнительного фактора x1 является существенным. Фактор х1 должен присутствовать в уравнении, в том числе в варианте, когда он дополнительно включается после фактора х2
Общий вывод состоит в том, что множественная модель с факторами х1 и х2 с R2yx1x2 = 0,9469 содержит неинформативный фактор х2. Если исключить фактор х2, то можно ограничиться уравнением парной регрессии:
ŷx = α0 + α1 · x = 1,99 + 1,23 · x, r2yx = 0,9407
более простым, хорошо детерминированным, пригодным для анализа и для прогноза.
6. Средние частные коэффициенты эластичности Эyx j показывают, на сколько процентов от значения своей средней у изменяется результат при изменении фактора xj, на 1% от своей средней xj и при фиксированном воздействии на у всех прочих факторов, включенных в уравнение регрессии. Для линейной зависимости
Эyx j = b j
| xj |
| y |
где bj - коэффициент регрессии при x1,- в уравнении множественной регрессии.
Здесь
Эyx1 =
| 0,9459·6,19 |
| 9,6 |
= 0,6099%
Эyx2 =
| 0,0856 · 22,3 |
| 9,6 |
= 0,1989%
По значениям частных коэффициентов эластичности можно сделать вывод о более сильном влиянии на результат у признака фактора x2 чем признака фактора х2: 0,6% против 0,2%.
Дата добавления: 2015-09-10; просмотров: 459 | Поможем написать вашу работу | Нарушение авторских прав |