Читайте также:
|
Пусть функция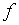 
непрерывна на отрезке 
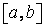(или интервале, полуинтервале). Тогда для каждой точки 
этого отрезка (интервала, полуинтервала) по заданному 
найдется 
такое, что
,
как только
.
При изменении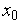 
при постоянном 
число 
, вообще говоря, изменяется – оно зависит не только от , но и от 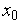. Как видно из рис. 29, число , пригодное на участке с пологим графиком, может оказаться слишком большим для участка с круто поднимающимся графиком.
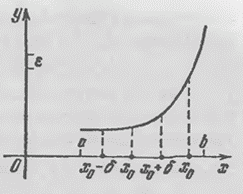
Рис. 29
В связи с этим естественно выделить те непрерывные функции, для которых при данном можно указать , пригодное сразу для всех 
, принадлежащих тому множеству, где задана функция.
Начнем с определения.
О п р е д е л е н и е 1. Функция 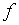, определенная на множестве 
, называется равномерно непрерывной на этом множестве, если для всякого найдется , зависящее только от 
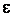, такое, что
для всех 
, удовлетворяющих неравенству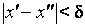 
.
Легко видеть, что если функция равномерно непрерывна на множестве , то тем более она равномерно непрерывна на любом его подмножестве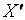 
. Обратное, вообще говоря, неверно.
Т е о р е м а 1. Если функция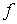 
определена и непрерывна на отрезке 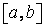, то она равномерно непрерывна на нем.
Д о к а з а т е л ь с т в о. Допустим, что теорема неверна. Тогда существует такое 
, что для любого найдется пара точек 
, удовлетворяющих неравенству 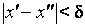, для которых
.
Зададим стремящуюся к нулю последовательность положительных чисел 
. Для каждого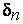 
найдутся точки 
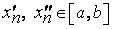такие, что
, но 
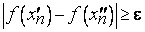. (1)
Так как последовательности 
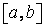принадлежат к , то эта последовательность ограничена и из нее по теореме Больцано-Вейерштрасса можно выделить подпоследовательность 
, сходящуюся к некоторой точке 
. Так как 
, 
, то подпоследовательность 
тоже сходится к точке 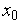. По условию функция 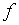непрерывна на 
и, следовательно, непрерывна в точке . Конечно, если 
или 
, то надо считать, что непрерывна в 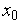справа или соответственно слева. Поэтому
.
После перехода к пределу в (1) при получим
, (2)
и мы пришли к противоречию: 
.
Заметим, что в (2) мы воспользовались непрерывностью функции 
(см. § 3.3, пример 8). Теорема доказана.
П р и м е р 1. Функция
непрерывна на отрезке 
, поэтому на основании теоремы 1 она равномерно непрерывна на этом отрезке.
С другой стороны, на полуинтервале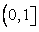 
эта функция хотя и непрерывна, но не является равномерно непрерывной. Это показывает, что требование в теореме 1, чтобы непрерывная функция была задана на отрезке, а не на интервале, существенно.
Убедимся в том, что наша функция не является равномерно непрерывной на 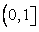. Точки 
, очевидно, принадлежат полуинтервалу 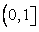, и для них
.
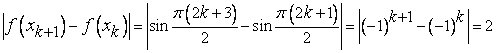Если задать 
, то при любом найдется такое 
, что
,
между тем как
.
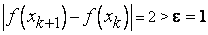Из сказанного следует, что нашу функцию нельзя продолжить на отрезок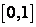 
, доопределив ее в точке 
так, чтобы она стала непрерывной на 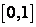, потому что тогда, согласно теореме 1, она была бы равномерно непрерывной на 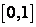, а следовательно, и на 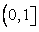, чего быть не может.
Точки разрыва и их классификация.
Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х0, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х0является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.
Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.
Если односторонний предел (см. выше)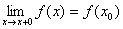 
, то функция называется непрерывной справа.
|
х0
Если односторонний предел (см. выше) 
, то функция называется непрерывной слева.
|
х0
Определение. Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.
Определение. Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.
Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее.
Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже.
Определение. Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
Пример. Функция Дирихле (Дирихле Петер Густав(1805-1859) – немецкий математик, член- корреспондент Петербургской АН 1837г)
не является непрерывной в любой точке х0.
Пример. Функция f(x) = 
имеет в точке х0 = 0 точку разрыва 2 – го рода, т.к.
.
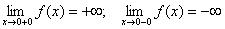Пример. f(x) =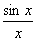 
Функция не определена в точке х = 0, но имеет в ней конечный предел 
, т.е. в точке х = 0 функция имеет точку разрыва 1 – го рода. Это – устранимая точка разрыва, т.к. если доопределить функцию:
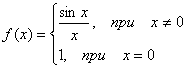
График этой функции:
Пример. f(x) =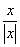 
= 
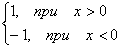
y
0 x
-1
Эта функция также обозначается sign(x) – знак х. В точке х = 0 функция не определена. Т.к. левый и правый пределы функции различны, то точка разрыва – 1 – го рода. Если доопределить функцию в точке х = 0, положив f(0) = 1, то функция будет непрерывна справа, если положить f(0) = -1, то функция будет непрерывной слева, если положить f(x) равное какому- либо числу, отличному от 1 или –1, то функция не будет непрерывна ни слева, ни справа, но во всех случаях тем не менее будет иметь в точке х = 0 разрыв 1 – го рода. В этом примере точка разрыва 1 – го рода не является устранимой.
Таким образом, для того, чтобы точка разрыва 1 – го рода была устранимой, необходимо, чтобы односторонние пределы справа и слева были конечны и равны, а функция была бы в этой точке не определена.
Дата добавления: 2015-09-10; просмотров: 176 | Поможем написать вашу работу | Нарушение авторских прав |