Читайте также:
|
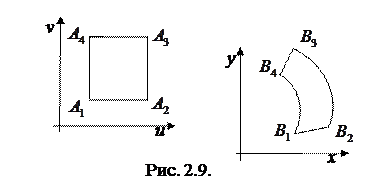Рассмотрим снова преобразование плоскости 
в плоскость 
, которые задаются формулами
Выделим на плоскости бесконечно малый прямоугольник со сторонами 
и 
параллельными осям 
и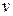 
. Изображением этого прямоугольника на плоскости будет криволинейный четырехугольник 
.
Определим его площадь.
Вершины прямоугольника на плоскости имеют координаты 
, 
, 
, 
. Тогда координаты вершин четырехугольника будут
, 
,
, 
.
Если ограничиться членами первого порядка малости относительно и , т.е. 
, 
, то приближенно можно взять точки 
, 
,
, 
где 
, 
и все производные вычислены в точке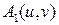 
.
Т.к. проекция отрезков 
и 
на обе оси соответственно равны
и 
то эти отрезки равны и параллельны, так что с точностью до бесконечно малых высшего порядка, четырехугольник есть параллелограмм, его площадь равна удвоенной площади треугольника 
.
Из аналитической геометрии известно, что если 
, 
, 
, то 
(по абсолютной величине), т.е. в нашем случае 
.
Так выражается элемент площади в криволинейных координатах.
Разбивая область 
(на плоскости ) прямыми, параллельными осям на бесконечно малые прямоугольники, мы одновременно разложим и фигуру 
на криволинейные четырехугольники рассмотренного вида. Суммируя выражения для их площадей, мы придем к формуле
Замечание. Знак функционального определителя 
указывает на направление обхода контура, если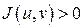 
, то при положительном обходе контура в области соответствующий контур в так же обходится в положительном направлении; 
, то положительному обходу контура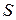 
соответствует отрицательный обход 
.
Из равенства 
, видно, что якобиан является коэффициентом растяжения площади при отображении плоскости на плоскость .
Дата добавления: 2015-09-10; просмотров: 114 | Поможем написать вашу работу | Нарушение авторских прав |