Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Вычисление двойного интеграла

Пусть требуется вычислить .

Рассмотрим случай, когда . Построим цилиндрическое тело , объем которого равен рассматриваемому интегралу

.

Пусть отрезки и являются проекциями области на координатные оси. Предположим, что всякая прямая, параллельная оси , пересекает границу области в двух точках (кроме прямых , ). Пусть уравнения «верхней» и «нижней» области и .

Зафиксируем точку 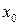() и проведем плоскость . Пересечение этой плоскости с телом дает плоскую пластину с площадью . Эта криволинейная трапеция с основанием и ограниченная дугой графика функции , причем аргумент меняется в пределах .

Значит, площадь этой криволинейной трапеции .

Меняя теперь 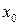в пределах от до , применим для определения объема тела формулу объема по площадям поперечных сечений

.

Заменяя в этом равенстве 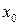на и учитывая, что , получим

.

Интеграл, стоящий в правой части, называется повторным.

Мы рассмотрели случай, когда граница области пересекается в двух точках прямыми, параллельными оси .

Аналогично, если тоже выполнено относительно оси 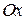(кроме прямых и ), а и – уравнения «левой» и «правой» частей границы соответственно, то рассуждая аналогично, получим

.

Исходя из и, получаем возможность изменять порядок интегрирования при вычислении повторных, и – как следствие – двойных интегралов

.

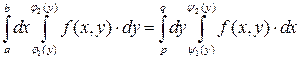Замечание. Следует отметить, что при вычислении повторных интегралов, сначала вычисляется внутренний интеграл по указанной переменной, считая другую переменную постоянной величиной, а затем после применения формулы Ньютона-Лейбница к внутреннему интегралу, интегрируем полученное выражение по указанной другой переменной.

Мы рассмотрели случай, когда .

Если же , то и

.

Но , т.е. получаем ту же формулу.

Пусть теперь - знакопеременная в .

Пусть в подобласти , в подобласти , и пусть - уравнение линии, разделяющей на и . Тогда

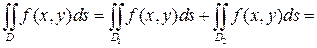
, т.е. формула справедлива и для знакопеременной функции.

И наконец, если область интегрирования более сложная, то ее следует разбить на части, для которых справедлива одна из формул и.