Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Вычисление тройных интегралов

Рассмотрим область , ограниченную снизу и сверху поверхностями и и цилиндрической поверхностью с образующими, параллельными оси . Пусть - проекция области на плоскость . Предположим, что любая прямая, параллельная оси , пересекает границу области не более чем в двух точках. Тогда для любой непрерывной в области функции имеет место формула

.

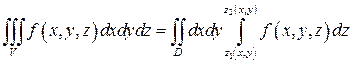По этой формуле сначала вычисляется внутренний однократный интеграл по переменной , при этом и рассматриваются как постоянные. Затем по изложенным в предыдущей теме правилам вычисляется двойной интеграл. Например, если область задается неравенствами , , 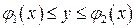то формулу можно переписать в виде

,

т.е. свести к последовательному вычислению трех определенных интегралов.

Если область не относится к рассмотренному типу, то ее всегда можно разбить на непересекающиеся части, для которых процесс сведения вычисления тройного интеграла к вычислению определенных интегралов возможен.

Следует заметить, что пределы интегрирования внешнего интеграла всегда постоянны. Пределы интегрирования во внутренних интегралах в формуле всегда переменны, за исключением случая, когда - параллелепипед с гранями , , , , , :

.

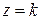Формулу можно записать в виде

,

где - сечение области плоскостью . Такая запись иногда удобнее, чем, в особенности, если достаточно легко описывается аналитически.

Отметим, что формулы допускают естественные обобщения на другой порядок интегрирования по переменным в кратных интегралах.