Читайте также:
|
По определению ротор (вихрь) некоторого вектора 
:
(36)
Зная ротор вектора в каждой точке некоторой (не обязательно плоской) поверхности S, можно вычислить циркуляцию этого вектора по контуру 
, ограничивающему S, (контур также может быть не плоским). Для этого разобъём поверхность на очень малые элементы 
. Ввиду их малости эти элементы можно считать плоскими. Поэтому в соответствии с (36) циркуляция вектора по контуру, ограничивающему , может быть представлена в виде.
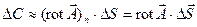(37)
где 
- положительная нормаль к элементу поверхности .
Зная, что циркуляция по некоторому контуру равна сумме циркуляций по контурам, содержащиеся в данном, можно просуммировать выражение (37) по всем , и тогда получим циркуляцию вектора по контуру , ограничивающему S:
.
Осуществив предельный переход, при котором все стремиться к нулю (число их при этом неограниченно растёт, придём к формуле:
(38)
Соотношение (38) носит название теоремы Стокса. Смысл её состоит в том, что циркуляция вектора по произвольному контуру равна потоку вектора 
через произвольную поверхность S, ограниченную данным контуром.
Дата добавления: 2015-09-11; просмотров: 90 | Поможем написать вашу работу | Нарушение авторских прав |