Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

И вектор Умова — Пойнтинга

Докажем тождество

div [Ж Ж] = Ж rot Ж - Ж rot If. Вычислим векторное произведение векторов Е и Япо

Раскроем скобки и сгруппируем полученные слагаемые следующим обра­зом:

div [if Я*] =

дЕ_у дЕ_х

dE_z дЕ_у

ду ~д7 dH_z

ду dz) * oz ox J \ дх ду

Как следует из формулы (10.20), первые три выражения в круглых скоб­ках, следующие за координатами вектора В, есть координаты вектора rot E,

дЕ_х ВЕ

выражения в круглых скобках, следующие за координатами векто­ра Е, есть координаты вектора rot Я. Таким образом, тождество (10.22) доказано.

Вычислим производную от плотности энергии w по времени t. Соглас­но формуле (10.11) с учетом формул (10.10) будем иметь

dt

Преобразуем pfo выражение при помощи уравнений (10.1) и (10.3), запи­
сав их в видеС-' dB

Получим

С учетом тождества (10.22) придем к уравнению

(10.23)

Чтобы доказать это, проинтегрируем обе части уравнения (10.23) по не­которому объему V. Получим

Левую часть этого равенства можно записать так:

где

■

W(t) = f

- энергия электромагнитного поля, заполняющая объем V в момент вре­мени t. Первый интеграл в правой части

Р- fjlfdV

v

есть мощность джоулева энерговыделения, т.е. тепло, которое выделя­ется в объеме V за единицу времени вследствие прохождения электри­ческого тока по веществу в этом объеме. Интеграл от дивергенции по объему V, используя теорему Остроградского - Гаусса, можно преобра­зовать в интеграл по поверхности S, ограничивающей этот объем:

Таким образом, придем к уравнению (10.14).

Ковариантность уравнений Максвелла

Можно показать, что уравнения Максвелла, описывающие электро­магнитное поле в вакууме, ковариантны относительно преобразований Лоренца. Это означает, что системы отсчета К к другой К'. Преобразованиям Лоренца соответствуют определенные преобразования величин, характеризующих электромагнитное поле. Пусть некоторое электромагнитное поле в системе отсчета К, характеризуется векторами

Е и В напряженностей электрического и магнитного полей. В

К' то же электромагнитное поле будет характеризоваться дру­гими векторами Е' и В'. При переходе от одной инерциальной системы отсчета к другой эти векторы преобразуются так, что

Ж'=

В результате оказывается, что электромагнитное поле, создаваемое од­ной и той же системой зарядов, описывается различными функциями

div 5* dV = i]Н -Н (t, r)

в разных инерциальных системах отсчета.

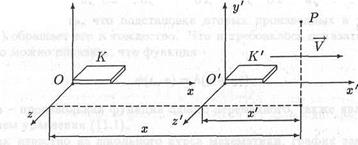
Рассмотрим два тела К и К'. Пусть второе тело движется относи­тельно первого прямолинейно и поступательно с постоянной скоростью V. Построим две прямоугольные декартовы системы координат К и К', связанные с этими телами (рис. 10.1). Событие А, произошедшее в неко­торой точке пространства Р, характеризуется наблюдателем в системе отсчета К координатами х, у и z этой точки и моментом времени t. Это же событие А характеризуется наблюдателем в системе отсчета К¹ ко­ординатами х', у' и z' точки Р и моментом времени t'. Связь между величинами х, у, z,t и х', у', z', t' осуществляется посредством преобра­зований Лоренца

где

Эти формулы описывают переход от одной инерциальной системы отсче­та к другой.

Рис. 10.1. Две инерциалъные системы отсчета