
Читайте также:
|
Кольцо с единицей не равной нулю, в котором каждый не нулевой элемент обратим называется телом. Коммутативное тело- поле. (F,+,*) 1) (F,+,*)-тело 2) ав=ва 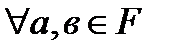
Свойства:
1)  2)
2)  3)
3)  4)
4)  5)
5) 
6) а+х=в => х=в-а; ах=в =>  7) na,
7) na, 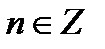 ;
; 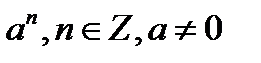
Примеры: 1) (Q,+,*) 2) (R,+,*) 3) (C,+,*) - бесконечные поля. 4) Пример конечного поля: (Z(p),+,*).
Поле классов вычетов: Теорема множество классов вычетов, где p- простое число- поле. Док-во: надо доказать, что у любого не нулевого элемента есть обратный.  , покажем, что все эти числа различные и не равны 0, в этом случае данное множество будет совпадать с
, покажем, что все эти числа различные и не равны 0, в этом случае данное множество будет совпадать с  , это будет означать, что
, это будет означать, что  1)
1)  от обратного,
от обратного,  а этого быть не может, т.к. p-простое, а m,a<p. 2)
а этого быть не может, т.к. p-простое, а m,a<p. 2) 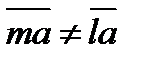 , 1< l, l <p-1 От обратного:
, 1< l, l <p-1 От обратного:  ,
,  не может такого быть.
не может такого быть.
Тело. Пример:
Кольцо с единицей не равной нулю, в котором каждый не нулевой элемент обратим называется телом.
(В,+,*)
1) (В,+)- абелево
2) (В\{0},*)- группа
3) дистрибутивность а(в+с)=ав+ас, (в+с)а=ва+са
Пример тела: Тело кватернионов Т={a+bi+cj+dk,a,b,c,d  R} i,j,k- мнимые единицы.
R} i,j,k- мнимые единицы. 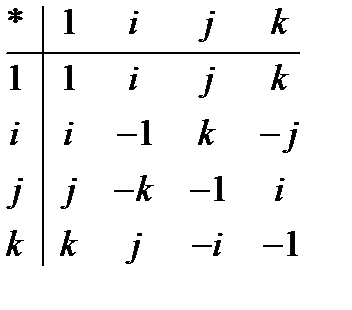 ;
; 
Дата добавления: 2015-09-11; просмотров: 97 | Поможем написать вашу работу | Нарушение авторских прав |