Читайте также:
|
Для вычисления определенного интеграла, когда можно найти соответствующий неопределенный интеграл, служит формула Ньютона-Лейбница 
.Применяя обозначение F(b) – F(a) = F(x) 
, где F(x) – первообразная для f(x), формулу Ньютона-Лейбница запишем в виде
Значение определенного интеграла равно разности значений любой первообразной от подынтегральной функции, взятой при вернем или нижнем пределах интегрирования. Вертикальная черта с верхним и нижним пределами, стоящая справа от символа функции F(x), называется знаком двойной подстановки.
Понятие определенного интеграла широко применяется для вычисления различных геометрических и физических величин.
Возможны следующие случаи:
1. Фигура ограничена графиком непрерывной и неотрицательной на отрезке [a; b] функции f(x) (f(x)≥0), осью Ox, прямыми x = a, x = b, тогда S = 
2. Фигура ограничены графиком непрерывной и неположительной на отрезке [a; b] функции f(x) (f(x)≥0), осью Ox, прямыми x = a, x = b, тогда S = 
3. Фигура ограничена осью Ox, прямыми x = a, x = b и графиком функции f(x), которая непрерывна на отрезке [a; b]и меняет свой знак конечное число раз на этом отрезке (Рис. 5). В этом случае разбивают отрезок [a; b] на такие частичные отрезки, на которых функция f(x) законопостоянна. Искомая площадь S численно равна алгебраической сумме интегралов, взятых по каждому из полученных отрезков, причем знаки, с которыми эти интеграл входят в алгебраическую сумму, совпадают со знаками функции f(x) на соответствующих отрезках. Площадь фигуры, изображенной на рис. 5, вычисляется по формуле S= 
3.Найти площадь фигуры, ограниченной линиями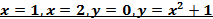 
.
Дата добавления: 2015-01-30; просмотров: 139 | Поможем написать вашу работу | Нарушение авторских прав |