
Читайте также:
|
Тригонометрическиетождества — математические выражения для тригонометрических функций, которые выполняются при всех значениях аргумента (из общей области определения).
Основные тригонометрические тождества
· sin² α + cos² α = 1
· tg α · ctg α = 1
· tg α = sin α ÷ cos α
· ctg α = cos α ÷ sin α
· 1 + tg² α = 1 ÷ cos² α
· 1 + ctg² α = 1 ÷ sin² α
Функция 
| Аргумент 
| |||||||||
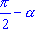
| 
| 
| 
| 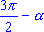
| 
| 
| 
| |||
sin 
| cos 
| cos 
| sin 
| -sin 
| -cos 
| -cos 
| -sin 
| sin 
| ||
cos 
| sin 
| -sin 
| -cos 
| -cos 
| -sin 
| sin 
| cos 
| cos 
| ||
tg 
| ctg 
| -ctg 
| -tg 
| tg 
| ctg 
| -ctg 
| -tg 
| tg 
| ||
ctg 
| tg 
| -tg 
| -ctg 
| ctg 
| tg 
| -tg 
| -ctg 
| ctg 
| ||
Заучивать эти формулы нет нужды. Достаточно помнить следующее:
1) если в формуле содержатся углы 180° и 360° (π и 2π), то наименование функции не изменяется;
если же в формуле содержатся углы 90° и 270° (π/2 и 3π/2), то наименование функции меняется на сходное (синус на косинус, тангенс на котангенс и т. д.);
2) чтобы определить знак в правой части формулы (+ или—), достаточно, считая угол φ острым, определить знак выражения, стоящего в левой части формулы.
Дата добавления: 2015-01-30; просмотров: 125 | Поможем написать вашу работу | Нарушение авторских прав |