Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Уравнения плоского движения твердого тела

Для задания положения плоской фигуры на плоскости относительно системы координат 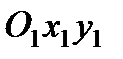, лежащей в плоскости фигуры, достаточно задать на этой плоскости положение отрезка АВ, скрепленного с фигурой.

Положение отрезка АВ, относительно системы координат 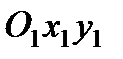определяется заданием координат какой-нибудь точки этого отрезка и его направления. Например, координаты точки А () и направление, заданное углом .

Уравнения движения плоской фигуры относительно системы координат 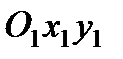имеют вид: .

Твердое тело при плоском движении имеет три степени свободы.

Функции

называются уравнениями плоского движения твердого тела.

Перейдем к изучению движения отдельной точки твердого тела. Положение любой точки М плоской фигуры относительно подвижной системы отсчета , скрепленной с этой движущейся фигурой и лежащей в ее плоскости, полностью определяется заданием координат x и y точки М (Рис.6-3).

Рис. 6-3

Между координатами точки М в различных системах отсчета существует связь:

, (6-1)

где - длина отрезка ОМ, - постоянный угол между ОМ и осью . С учетом выражений и получаем

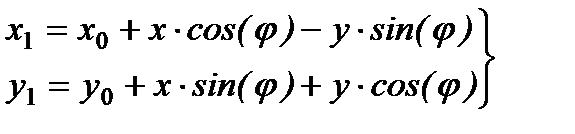, (6-2)

Формулы (6-2) являются уравнениями движения точки М плоской фигуры относительно координат 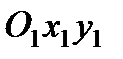. Эти формулы позволяют определить координаты любой точки плоской фигуры по заданным уравнениям движения этой фигуры и координатам этой точки относительно подвижной системы отсчета, скрепленной с движущейся фигурой.

Используя матрично-векторные обозначения уравнения (6-2) можно записать в такой форме:

,

где А – матрица поворота на плоскости:

, , , .