Читайте также:
|
Теоретической основой алгоритма отделения корней служит теорема Коши о промежуточных значениях непрерывной функции:
Теорема 2.1. Если функция f (x) непрерывна на отрезке [ a, b ] и f (a) = A, f (b) = B, то для любой точки C, лежащей между A и B на этом отрезке существует точка 
, что f (ξ) = C.
Следствие. Если функция f (x) непрерывна на отрезке [ a, b ] и на его концах принимает значения разных знаков, то на этом отрезке существует хотя бы один корень уравнения f (x) = 0.
Пусть область определения и непрерывности функции является конечным отрезком [ a, b ]. Разделим отрезок на n частей:
ak = a + kh, k = 0, 1, … n, h = (b – a)/ n.
Вычисляя последовательно значения функции в точках a 0, a 1, … an, находим такие отрезки [ ak, ak +1], для которых выполняется условие
f (ak)∙ f (ak +1) < 0, (2.1)
Теорема 2.2. Если непрерывная функция f (x) монотонна на отрезке
[ a, b ] и на его концах принимает значения разных знаков, то на этом отрезке существует единственный корень уравнения f (x) = 0.
Если функция f (x) дифференцируема и её производная сохраняет знак на отрезке [ a, b ], то f (x) монотонна на этом отрезке.
Если производная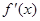 
легко вычисляется и нетрудно определить её корни, то для отделения корней уравнения f (x) = 0 можно применить следующий алгоритм:
1) Найти критические точки, т.е. точки, в которых производная 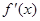равна нулю или не существует, и определить интервалы знакопостоянства производной 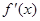(на этих интервалах функция f (x) может иметь только по одному корню);
2) Составить таблицу знаков функции f (x), приравнивая переменную x критическим и граничным значениям, или близким к ним;
3) Определить отрезки, на концах которых функция принимает значения разных знаков.
Дата добавления: 2015-02-16; просмотров: 106 | Поможем написать вашу работу | Нарушение авторских прав |