Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Приближение функций

Если требуется найти способ приближенного вычисления значения функции в заданной точке.

Например, функция f (x) определяется как решение сложной задачи. Здесь могут быть известны некоторые свойства функции y = f (x), например, непрерывность и дифференцируемость.

Даже если функция легко вычисляется, может возникнуть необходимость её замены, например, при вычислении некоторых определенных интегралов или специальных функций математической физики (ниже будут приведены примеры). В этом случае вместо подынтегральной функции надо подобрать другую функцию, от которой интеграл легко вычисляется. Разумеется, эта новая функция должна быть приближенно равна в некотором смысле подынтегральной функции.

Если значения функции определяются в результате дорогостоящих экспериментов, могут быть найдены её значения только в некоторых точках, а для вычисления значения в произвольной точке требуется приближенный метод. При этом может быть известен вид функции, но неизвестны параметры, входящие в определение функции. В этом случае задача сводится к определению параметров известной функции.

Аппроксимацией (приближением) функции f (x) называется нахождение такой функции g (x) (аппроксимирующей функции), которая была бы близка заданной. Критерии близости функций могут быть различные.

В том случае, когда приближение строится на дискретном наборе точек(x_i, y_i), i = 1, 2, …, n, аппроксимацию называют точечной или дискретной.

При точечной квадратичной аппроксимации параметры a ₁, a ₂, …, a_m аппроксимирующей функции g = g (x, a ₁, a ₂, …, a_m), m ≤ n, определяются из условия:

.

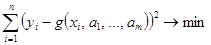Если аппроксимация проводится на непрерывном множестве точек (отрезке), аппроксимация называется непрерывной или интегральной.

При интегральной квадратичной аппроксимации функции y = f (x) на отрезке [ a _, b ] параметры аппроксимирующей функции g (x, a ₁, a ₂, …, a_m) определяются из условия:

Примером непрерывной аппроксимации может служить использование конечного числа слагаемых разложения функции в ряд Тейлора, то есть замена функции многочленом.

Наиболее часто встречающимся видом точечной аппроксимации на дискретном наборе из (n + 1)-й точки(x_i, y_i), i = 0, 1, …, n является интерполяция многочленом n -го порядка P_n (x), коэффициенты которого определяются из условий

y_i = P_n (x_i), i = 0, 1, … n.

Применяя интерполяционный многочлен, можно вычислить значения функции f (x) между узлами (провести интерполяцию в узком смысле), а также определить значение функции за пределами заданного интервала (провести экстраполяцию). Следует иметь в виду, что погрешность экстраполяции может быть велика.

В том случае, когда интерполяционный многочлен един для всей области интерполяции, говорят, что интерполяция глобальная. Если между различными узлами интерполяционные многочлены различны, говорят о кусочной или локальной интерполяции. Простейшим случаем локальной интерполяции является кусочно-линейная интерполяция, когда в качестве интерполяционной функции выбирается полином первой степени, то есть узловые точки соединяются отрезками прямой.