Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Розв’язання проблеми для "-формул і $-формул.

Під "-формулою розуміють формулу , у якої в пренексній нормальній формі кванторна частина містить лише квантори загальності, а під $-формулою розуміють формулу 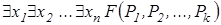, у якої в пренексній нормальній формі кванторна частина містить лише квантори існування, причому Р_і= Р_і (х₁, х₁, …, х₁), і=1, 2, …, k.

Теорема 13.6. "-формула загальнозначуща тоді й тільки тоді, коли вона тотожно істина на n -елементній множині.

Доведення. Нехай дана формула тотожно істинна на деякій n -елементній множині. Тоді вона тотожно істинна на довільній n -елементній множині (тому що ці множини ізоморфні). Тоді на будь-якій n -елементній множині тотожно істинна формула . Розглянемо тепер інтерпретацію на довільній множині: Р₁= А₁, …, Р_k=A_k. Одержимо конкретний предикат , який залежить від n -змінних. Підставляючи замість них конкретні предмети, ми фактично маємо справу з n -елементною множиною, на якій цей предикат тотожно істинний. Отже, він буде тотожно істинним і на всій цій множині. Таким чином формула тотожно істинна на любій множині, а разом з нею тотожно істинна на любій множині, тобто загальнозначуща, й формула .

Теорема 13.7. $-формула 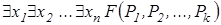загальнозначуща тоді й тільки тоді, коли вона тотожно істинна на одноелементній множині.

Доведення даної теореми анологічне доведенню попередньої теореми.

Таким чином, проблема виконуваності й загальнозначущості формул логіки предикатів є достатньо складною й, в загальному, не розв’язаною до кінця проблемою.