Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Доказательство.

Докажем это свойство методом математической индукции.

Для определителя 2 – го порядка утверждение выполняется. Действительно,

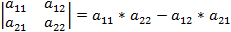
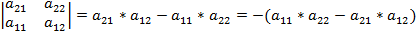
Будем считать, что свойство справедливо для определителя (n – 1) – го порядка. Докажем, что оно справедливо и для определителя n – го порядка.

1) Пусть в определителе (2.2) переставляются i – ая и k – ая строки, а все остальные строки остаются на месте и i ≠ 1, k ≠ 1.

Мы получаем определитель

(2.6)

Сбоку указаны номера строк в определителе (2.2). Разложим определитель (2.6) по элементам первой строки (формула (2.3)).

det А' = a₁₁А₁₁ + a₁₂А₁₂ + … + a_1nА_1n,

при этом А₁₁ = (-1)¹⁺¹ М₁₁, А₁₂ = (-1)¹⁺² М₁₂, … А_1n = (-1)¹⁺ⁿ М_1n

Все миноры М₁₁, М₁₂, … М_1n определителя (2.6) отличаются от соответствующих миноров определителя (2.2) тем, что в них поменялись местами i – ая и k – ая строки. Так как все эти миноры являются определителями (n – 1) – го порядка, то на основании индуктивного предположения знак их изменится на противоположный. Поэтому изменится знак у всех алгебраических дополнений и, мы, окончательно, получим det А = – det А'.

2) Пусть теперь в определителе (2.2) переставляются местами первая строка и любая другая. Например, i = 1, k ≠ 1. Все остальные строки остаются на месте. Получим определитель (2.6'), выписывать который нет необходимости. Для вычисления определителя (2.6') используем формулу (2.5) разложения определителя по элементам 1 – го столбца. И в этом случае все алгебраические дополнения А₁₁, А₂₁, … А_n1 определителя (2.6') будут отличаться знаком от соответствующих алгебраических дополнений определителя (2.2). Поэтому det А = – det А'.

Для пояснения сказанного, рассмотрим конкретный пример, с тем, чтобы выяснить, отчего в случае 2) может произойти изменение знака алгебраических элементов 1 – го столбца.

Пусть дан определитель

Разложим его по элементам 1 – го столбца

Переставим местами первую и третью строку в определителе и разложим полученный определитель по элементам 1 – го столбца

Знак у алгебраических дополнений А₁₁ и А₂₁ изменяется на противоположный оттого, что изменяется знак у множителей (-1)^i+j этих алгебраических дополнений. У алгебраических дополнений А₃₄ и А₄₁ знак изменяется на противоположный оттого, что в минорах М₃₁ и М₄₁ поменялись местами две строки.