Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Доказательство

Система однородных уравнений совместна, так как имеет тривиальное решение. Поэтому она равносильна разрешенной системе, в которой число уравнений r ≤ m < n. Следовательно, данная система однородных уравнений является неопределенной и помимо тривиального решения имеет также ненулевые решения, в которых значения некоторых или всех неизвестных отличны от нуля.

*Символ ∑ употребляется для сокращенной записи суммы большого числа слагаемых одного и того же вида, отличающихся только индексами. Индекс j называется индексом суммирования.

Замечание 2.

Чтобы записать систему (1.2), нужно знать коэффициенты системы уравнений и свободные члены уравнений.

Выпишем их в виде следующей таблицы:

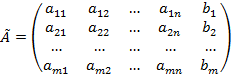
Получили таблицу из чисел, которая содержит m строк и (n + 1) столбец. Всякая прямоугольная таблица из чисел называется матрицей. Числа, составляющие матрицы, называются ее элементами. Элементы первых n столбцов имеют два индекса. Первый указывает номер строки, а второй - номер столбца. Например, элемент a_ij находится в i -ой строке и j -ом столбце.

Матрица называется расширенной матрицей системы уравнений (1.2). Она получается присоединением к матрице A из коэффициентов системы (1.2) столбца свободных членов. По матрице система (1.2) полностью восстанавливается.

Таблица Гаусса.

Расчеты по методу Жордана-Гаусса удобно располагать в так называемых таблицах Гаусса. В заглавной строке таблицы указываются неизвестные, а далее располагаются элементы расширенной матрицы системы уравнений.

Строки таблицы будем рассматривать как соответствующие уравнения данной системы и, выполняя этапы расчета, будем преобразовывать элементы строк таблицы.

Запишем систему уравнений (1.2) в виде таблицы 1.

Табл. 1 (исходная):

Разрешим систему (1.2) относительно неизвестной x_k.

Как и в §3, возьмем за разрешающий элемент a_sk ≠ 0, s -ю строку и k -ый столбец таблицы, на пересечении которых находится элемент a_sk будем называть разрешающей строкой и разрешающим столбцом.

Табл. 2.

Табл. 2 получим из табл. 1, умножив разрешающую строку на число .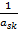

Элементы остальных строк переписали из табл. 1 без изменений.

Табл. 3.

x1	x2	…	xj	…	xk	…	xn	b
		…		…	0	…
…	…	…	…	…	…	…	…	…
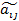
		…		…	0	…
…	…	…	…	…	…	…	…	…
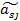
		…		…	1	…
…	…	…	…	…	…	…	…	…
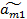
		…		…	0	…

В табл. 3 записана система линейных уравнений (1.12), разрешенная относительно x_k. Элементы всех строк таблицы, кроме разрешающей s -ой строки преобразованы по формулам (1.11). Расчеты по формуле (1.11) удобно проводить при помощи так называемого «правила прямоугольника», использую табл. 2. Например, чтобы вычислить преобразованный элемент выделим в табл. 2 разрешающие строку и столбец и рассмотрим «прямоугольник» в вершинах которого находятся элементы , .

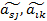Согласно (1.11), чтобы вычислить преобразованный элемент нужно из элемента вычесть произведение элементов, находящихся в соседних с элементом вершинах «прямоугольника», т. е. = – * .

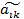Точно так же по «правилу прямоугольника» преобразуются элементы столбца свободных членов: .

Решение системы линейных уравнений при использовании таблиц Гаусса включает ряд последовательных этапов расчета.

Каждый этап состоит из следующих трех пунктов.

п. 1. В исходную таблицу записывается расширенная матрица системы уравнений и выбирается отличный от нуля разрешающий элемент и, тем самым, разрешающие строка и столбец.

п. 2. Элементы разрешающей строки умножаются на число, обратное разрешающему элементу и заносятся в таблицу 1 данного этапа расчета. Элементы остальных строк переписываются из исходной таблицы без изменений.

п. 3. В таблицу 2 данного этапа расчета переписывается разрешающая строка из предыдущей таблицы 1. В разрешающем столбце записываются нули, кроме 1 в разрешающей строке. Элементы остальных строк вычисляются по «правилу прямоугольника», используя таблицу 1.

На этом заканчивается выполнение первого этапа преобразований, после чего расчет повторяется с п. 1, при этом исходной таблицей очередного этапа расчета является последняя таблица предыдущего этапа. Перед выполнением очередного этапа из таблицы вычеркиваются все строки, состоящие из одних нулей.