
Читайте также:
|
При помощи элементарных преобразований системы линейных уравнений можно добиться того, что какая-либо неизвестная  будет входить только в одно уравнение системы с коэффициентом, равным 1, и отсутствовать во всех остальных уравнениях (в остальных уравнениях системы коэффициенты при
будет входить только в одно уравнение системы с коэффициентом, равным 1, и отсутствовать во всех остальных уравнениях (в остальных уравнениях системы коэффициенты при  будут равны нулю).
будут равны нулю).
В таком случае система линейных уравнений называется разрешенной относительно неизвестной  , а неизвестное
, а неизвестное  называется разрешенным.
называется разрешенным.
Разрешим систему линейных уравнений (1. 2) относительно неизвестной  .
.
Среди коэффициентов системы (1. 2) выберем любой отличный от нуля коэффициент при неизвестной  . Пусть
. Пусть 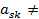 0.
0.  будем называть разрешающим коэффициентом, а уравнением с номером s - разрешающим уравнением.
будем называть разрешающим коэффициентом, а уравнением с номером s - разрешающим уравнением.
Выполним следующие элементарные преобразования системы (1. 2):
1) Умножим обе части разрешающего уравнения на число 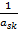 , т.е. выполним элементарное преобразование 2о.
, т.е. выполним элементарное преобразование 2о.
В результате коэффициент при неизвестной  станет равным единице, и уравнение примет вид
станет равным единице, и уравнение примет вид  (1. 10),
(1. 10),
где  .
.
2) При помощи уравнения (1. 10) исключим неизвестное  из всех остальных уравнений системы (1. 2). Чтобы исключить
из всех остальных уравнений системы (1. 2). Чтобы исключить  из i -огоуравнения системы, умножим уравнение (1. 10) на
из i -огоуравнения системы, умножим уравнение (1. 10) на  и сложим с i -ым уравнением, т.е. выполним элементарное преобразование 3о. В результате, i -оеуравнение не будет содержать неизвестную
и сложим с i -ым уравнением, т.е. выполним элементарное преобразование 3о. В результате, i -оеуравнение не будет содержать неизвестную  . Преобразуем i -ое уравнение:
. Преобразуем i -ое уравнение:
 (1. 11)
(1. 11)

 .
.
Точно так же как и для уравнения с номером i исключим  из всех других уравнений системы (1.2).
из всех других уравнений системы (1.2).
Получим, окончательно, систему уравнений:
 ,
,
эквивалентную исходной.
В системе (1. 12) неизвестное  входит только в s - ое уравнение с коэффициентом, равным единице и отсутствует в остальных уравнениях, т.е. система (1. 12) является разрешенной относительно неизвестной
входит только в s - ое уравнение с коэффициентом, равным единице и отсутствует в остальных уравнениях, т.е. система (1. 12) является разрешенной относительно неизвестной  . Коэффициенты системы (1. 12) и свободные члены уравнений, кроме разрешающего, вычисляются по формулам (1. 11), а для разрешающего уравнения по формулам (1. 10).
. Коэффициенты системы (1. 12) и свободные члены уравнений, кроме разрешающего, вычисляются по формулам (1. 11), а для разрешающего уравнения по формулам (1. 10).
Дата добавления: 2015-04-20; просмотров: 107 | Поможем написать вашу работу | Нарушение авторских прав |