Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Повторные независимые испытания. Формула Бернулли. Полиномиальное распределение. Формула Пуассона.

· Повторные независимые испытания

С понятием независимых событий связано понятие независимых испытаний опытов. Несколько опытов называются независимыми, если их исходы представляют собой независимые события.

Если опыт выполняется при данном комплексе условий многократно, причем вероятность наступления событий не зависит от исходов других испытаний, то такие испытания называются повторными независимыми испытаниями.

Пусть дана задача: Игральный кубик бросают 3 раза. Какова вероятность того, что из 3-х бросков 5-ка выпадет ровно 2 раза.

p=1/6; q=5/6

= ppq + pqp + qpp = 3p²q = 0.069

· Формула Бернулли

Теорема: если производится n независимых испытаний в каждом из которых вероятность появления события А равна р, а вероятность не появления соб. А равна q=1– p, то вероятность того, что событие А произойдет ровно m раз равна:

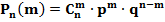(1)

где m =0,1,2,3…

· Полиномиальное распределение

Теорема: пусть дана серия из n независимых опытов, в каждом из которых может произойти k событий: А₁, А₂ ,…, А_k с вероятностями: p₁, p₂ ,…,p_k, тогда вероятность того, что событие А₁ появится m₁ раз, событие А₂ – m₂ раз … событие А_k – m_k раз равна:

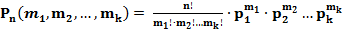(2) где m₁+ m₂…+ m_k = n

Пример на формулу Бернулли:

Производят 3 независимых выстрела по цели, вероятности попадания при разных выстрела одинаковы и равны 0.9, какова вероятность: а) 3-х промахов; б) одного попадания; в) 2-х попаданий; г) 3-х попаданий?

p=0.9; q=0.1

a)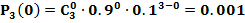

б)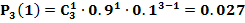

в)

г)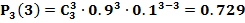

· Формула Пуассона

Использование формулы Бернулли при больших m и n вызывает трудности в связи с громоздкими вычислениями. В этом случае возникает необходимость отыскания приближенных формул для вычисления вероятности 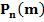обеспечивающих требуемую точность.

Теорема: если число испытаний неограниченно увеличивается ( 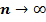), а вероятность (p) появления события А в каждом испытании неограниченно уменьшается, но так, что их произведение np=const=a, то вероятность того, что событие А случится ровно m раз приближенно равна:

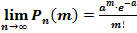(3)

· Приближенная формула Пуассона

Выражение (3) называют асимптотической формулой Пуассона. Обычно используется приближенное значение формулы (3) при достаточно больших значениях n и малом p.

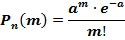
где a=np – параметр распределения Пуассона

Локальная и интегральная теоремы Муавра-Лапласа

В тех случаях когда число испытаний n велико а вероятность Р не близки к 0 или 1 (Р≠0; Р≠1) то для вычисления феноменальной вероятности используется форма Муавра-Лапласа

Теорема: (Локальная теорема Муавра-Лапласа)

Если вероятность Р наступления события А в каждом испытании постоянна и отлична от 0 и 1 а число испытаний достаточно велико то вероятность Рn(m) может быть вычислена по приближенной формуле:

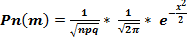(1)

Где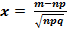

Чем больше n Тем точнее равенство (1)

Выражение (2) называется функцией Гауса, а ее график называется кривой вероятностью.

(3)

Для функции 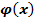составлены специальные таблицы.

Пример:

Вероятность попадания в мишень при одном выстреле равна 0,7. Найти вероятность того что при 200 выстреле мишень будет равна 160 раз.

n=200

p=0,7

m=160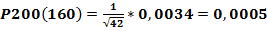

В тех случаях когда требуется вычислить вероятность того что в n – испытаниях событие A появится не менее K₁ но не более K₂ раз используют интегральную теорию Лапласа.

Теорема: (Интегральная теорема Муавра – Лапласа)

Если вероятность Р наступления события А в каждом испытании постоянна и отлична от 0 и 1 то вероятность Pn(K₁ ≤ m ≤ K₂) вычисляется по формуле:

(4)

Где ;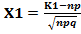

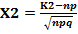
Чем больше число n тем точнее формула (4)

Используя функцию Гауса можно записать:

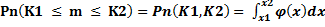(5)

Однако для условия вычислений при использовании формулы (4) вводят специальные функции:

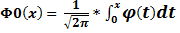(6)

(7)

Называется соответственно нормированной функцией Лапласа и функция Лапласа

Для этих функций также составлены таблицы.