Читайте также:
|
1.3.1. Определение частной производной и её геометрический смысл
Пусть дана функция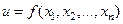 
. Зафиксируем все переменные, кроме одной 
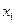, а переменной 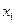дадим приращение 
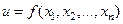, тогда получим частное приращение функции по переменной :
- 
.
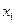Определение. Частной производной функции 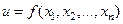по переменной 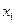называется предел отношения частного приращения этой функции по переменной 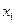к приращению этой переменной , при → 
= 
= 
.
Частную производную обозначают и другими символами: 
.
Вычислять частную производную функции многих переменных по одному аргументу следует по обычным правилам и формулам дифференцирования, в предположении, что все остальные аргументы - постоянные величины.
Пример.
Найти частные производные функции 
по аргументам 
и 
.
Считая постоянной, находим: 
;
считая постоянной, находим: 
.
Частная производная 
функции двух переменных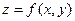 
, вычисленная по переменной в фиксированной 
выражает скорость изменения данной функции в направлении оси Ox или скорость изменения функции 
одной переменной .
Частные производные функции 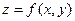в точке имеют следующий геометрический смысл: 
и 
, где α- угол между осью Ox и касательной, проведенной в точке 
к линии пересечения поверхности 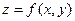и плоскости 
, β – угол между осью Oy и касательной в той же точке к линии пересечения поверхности 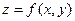и плоскости 
.
Дата добавления: 2015-09-10; просмотров: 97 | Поможем написать вашу работу | Нарушение авторских прав |