
Читайте также:
|
Определенным интегралом от a до b непрерывной функции y=f(x),определенной на интервале  a;b
a;b  , называется прирощение первообразной F(x) для этой функции,то есть
, называется прирощение первообразной F(x) для этой функции,то есть  baf(x)dx=F(b)−F(a)=F(x)ba.Числа a и b называются нижним и верхним пределами интегрирования. Физический смысл определенного интеграла:Путь S,пройденный телом при прямолинейном движении со скоростью v(t) за интервал времени от t 1 до t 2, вычисляется по формуле S =
baf(x)dx=F(b)−F(a)=F(x)ba.Числа a и b называются нижним и верхним пределами интегрирования. Физический смысл определенного интеграла:Путь S,пройденный телом при прямолинейном движении со скоростью v(t) за интервал времени от t 1 до t 2, вычисляется по формуле S =  t 2 t 1 v (t) dt. Геометрический смысл определенного интеграла:Площать S криволинейной трапеции (фируры, ограниченной графиком непрерывной положительной на интервале a; b функции y = f (x), осью OX и прямыми x = a и x = b) вычисляется по формуле S =
t 2 t 1 v (t) dt. Геометрический смысл определенного интеграла:Площать S криволинейной трапеции (фируры, ограниченной графиком непрерывной положительной на интервале a; b функции y = f (x), осью OX и прямыми x = a и x = b) вычисляется по формуле S =  baf (x) dx
baf (x) dx
8. Теорема Лагранжа. Формула Ньютона-Лейбница и её свойства.
Теорема Лагранжа Если функция f(x) определена и непрерывна на отрезке [a, b], то внутри отрезка ab обязательно отыщется(найдется) по крайней мере одна точка xc, такая, что выполняет равенство  . Это означает, что если на некотором промежутке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке. Определение. Выражение
. Это означает, что если на некотором промежутке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке. Определение. Выражение  называетсяформулой Лагранжаилиформулой конечных приращений.Чтобырешить определенный интеграл,надо сначала вычислитьнеопределенный интеграл(или найти первообразную), а затем вычислить определенный интеграл, подставив первообразную подынтегральной функции в формулу Ньютона-Лейбница:
называетсяформулой Лагранжаилиформулой конечных приращений.Чтобырешить определенный интеграл,надо сначала вычислитьнеопределенный интеграл(или найти первообразную), а затем вычислить определенный интеграл, подставив первообразную подынтегральной функции в формулу Ньютона-Лейбница: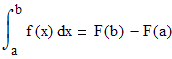
 .
.
Дата добавления: 2015-01-30; просмотров: 91 | Поможем написать вашу работу | Нарушение авторских прав |