Читайте также:
|
Якщо частина має масу і вагу починає падати під дією сили власної ваги, то швидкість її руху напочатку зростає в часі. Якщо не було б опору, то швидкість зростала б по відомому закону.
W=qt
Однак з ростом швидкості буде рости і сила опору середовища, а її прискорення буде зменшуватися. Через певний проміжок часу наступить динамічна рівновага: сила ваги стане рівною силі опору середовища. З цього моменту прискорення руху стане рівним нулеві і частина почне рухатися рівномірно з постійною швидкістю. Швидкість такого рівномірного руху називають швидкістю осадження Wос.
Сила, що заставляє частину рухатися рівна різниці сил ваги і архімедової сили, яка направлена протилежно до дії сили ваги.
Архімедова сила рівна вазі рідини, що витісняється тілом.
Різниця сил складає
r–густина середовища кг/м3
Сила опору середовища
Швидкість осадження Wос можна знайти із умови рівності сили, що рухає частину і сили опору середовища
Звідки
Підставляючи значення x в рівняння швидкості осадження отримуємо:
– Ламінарний режим
m – вязкість середовища, Па.С.
Максимальний розмір частинии, яка буде осідати по закону Стокса, якщо можна знайти, замість швидкості осадження в рівняння підставивши її значення, прийнявши Re=2 (граничне значення для ламінарної області)
, 
, 
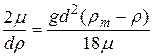
Існує і мінімальний розмір частин, нижче якого спостерігається відхилення від закону Стокса. Нижча границя застосування закону Стокса відповідає Re≈10-4
При Re<104 на швидкість осадження дуже дрібних частин починає впливати тепловий рух молекул середовища.
В повітрі, якщо частини мають розмір порядка 3 мкм, їх осадження не відбувається.
В перехідній області
2<Re<500
для знаходження швидкості осадження використовується залежність
замість величини опору середовища x підставляємо її значення.
В автомодельній області, коли Re не впливає на величину опору середовища
x=0,44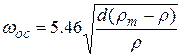 
Але щоб скористатися даними рівняннями для визначення швидкості осадження Wос необхідно знати величину критерія Re в який входить ця величина. У зв’язку з цим виникають ускладнення з вибором рівняння за яким можна розрахувати швидкість осадження.
Для знаходження Wос придатний тільки метод послідовних наближень, який є дуже трудомісткий. Тому для визначення Wос зручніше скористатись іншим методом, запропонованим П.В.Лященко. Цей метод базується на перетворенні основного рівняння для визначення Wос.
Піднімаємо обидві частини рівняння до квадрату
, 
Вираз правої частини суттєво не відрізняється від величини критерія Архімеда 
Підставивши в дане рівняння значення, яке характеризує певну область осадження отримаємо.
Для ламінарного осадження (закон Стокса)Re=Ar/2
Граничне значення Аг кр = 18•2 = 36.
Для перехідної області Re = 0,152 Аг0,715
Аг кр = 83000
Для автомодельної області
Аг>83000, x=0,44
Re=1,74 Ö Аг
Таким чином розрахувавши величину критерія Аг визначають область осадження, і тоді використовують одну із залежностей для розрахунку величини критерія Re, а відтак і швидкості осадження Wос.
Для розрахунків Wос може бути використана і єдина інтерполяційна залежність
Приведені рівняння справедливі для вільного осадження.
При великій концентрації твердої фази відбувається “Стиснене” осадження, швидкість якого менша від швидкості при вільному осадженні.
Дата добавления: 2015-04-12; просмотров: 12 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | <== 48 ==> | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 |